题目内容
某电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独闯第一关、第二关、第三关成功的概率分别为
,
,
,记该参加者闯三关所得总分为ζ.
(Ⅰ)求该参加者有资格闯第三关的概率;
(Ⅱ)求ζ的分布列.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
(Ⅰ)求该参加者有资格闯第三关的概率;
(Ⅱ)求ζ的分布列.
分析:(Ⅰ)根据游戏规定前两关至少过一关才有资格闯第三关,可求该参加者有资格闯第三关的概率;
(Ⅱ)由题意可知,ξ的可能取值为0,3,6,7,10,求出相应的概率,从而可求ζ的分布列.
(Ⅱ)由题意可知,ξ的可能取值为0,3,6,7,10,求出相应的概率,从而可求ζ的分布列.
解答:解:(Ⅰ)设该参加者单独闯第一关、第二关、第三关成功的概率分别为p1=
,p2=
,p3=
,
该参加者有资格闯第三关为事件A.则P(A)=p1(1-p2)+(1-p1)p2+p1p2=
. (4分)
(Ⅱ)由题意可知,ξ的可能取值为0,3,6,7,10,P(ξ=0)=(1-p1)(1-p2)=
,P(ξ=3)=p1(1-p2)(1-p3)+(1-p1)p2(1-p3)=
+
=
,P(ξ=6)=p1p2(1-p3)=
,P(ξ=7)=p1(1-p2)p3+(1-p1)p2p3=
+
=
,P(ξ=10)=p1p2p3=
,
所以ξ的分布列为
(12分)
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
该参加者有资格闯第三关为事件A.则P(A)=p1(1-p2)+(1-p1)p2+p1p2=
| 2 |
| 3 |
(Ⅱ)由题意可知,ξ的可能取值为0,3,6,7,10,P(ξ=0)=(1-p1)(1-p2)=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 8 |
| 3 |
| 8 |
| 1 |
| 8 |
| 1 |
| 12 |
| 1 |
| 24 |
| 1 |
| 8 |
| 1 |
| 24 |
所以ξ的分布列为
| ξ | 0 | 3 | 6 | 7 | 10 | ||||||||||
| p |
|
|
|
|
|
点评:本题考查概率的计算,考查随机变量的分布列,考查学生的计算能力,正确求概率是关键.

练习册系列答案
相关题目
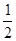 ,
,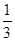 ,
,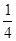 ,记该参加者闯三关所得总分为ζ.
,记该参加者闯三关所得总分为ζ.