题目内容
【题目】已知等差数列{an}的前n项和为Sn , 且a3=5,S15=225.数列{bn}是等比数列,b3=a2+a3 , b2b5=128(其中n=1,2,3,…). (Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=anbn , 求数列cn前n项和Tn .
【答案】解:(I)公差为d, 则 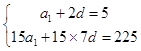 ,
,
∴ ![]() 故an=2n﹣1(n=1,2,3,…).
故an=2n﹣1(n=1,2,3,…).
设等比数列bn的公比为q,则 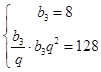 ,∴b3=8,q=2
,∴b3=8,q=2
∴bn=b3qn﹣3=2n(n=1,2,3,…).
(II)∵cn=(2n﹣1)2n∵Tn=2+322+523+…+(2n﹣1)2n
2Tn=22+323+524+…+(2n﹣3)2n+(2n﹣1)2n+1
作差:﹣Tn=2+23+24+25+…+2n+1﹣(2n﹣1)2n+1
= ![]()
=2+23(2n﹣1﹣1)﹣(2n﹣1)2n+1=2+2n+2﹣8﹣2n+2n+2n+1=﹣6﹣2n+1(2n﹣3)
∴TN=(2n﹣3)2n+1+6(n=1,2,3,…)
【解析】(I)在数列{an}中,把已知条件用首项a1 , 公差d表示,联立方程可求a1和d;在数列{bn}中,用b1和公比q把已知表示,求出b1和公比q(II)由(I)可知cn=(2n﹣1)2n , 利用错位相减求出数列的和
【考点精析】利用数列的前n项和对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系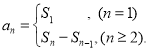 .
.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】某互联网理财平台为增加平台活跃度决定举行邀请好友拿奖励活动,规则是每邀请一位好友在该平台注册,并购买至少1万元的12月定期,邀请人可获得现金及红包奖励,现金奖励为被邀请人理财金额的![]() ,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
理财金额 |
|
|
|
乙理财相应金额的概率 |
|
|
|
丙理财相应金额的概率 |
|
|
|
(1)求乙、丙理财金额之和不少于5万元的概率;
(2)若甲获得奖励为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.