题目内容
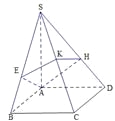
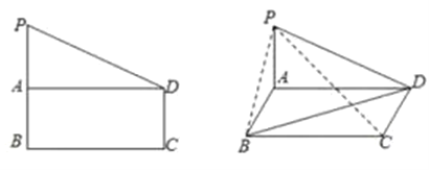
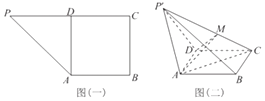
【题目】如图(一),在直角梯形ABCP中,CP∥AB,CP⊥BC,AB=BC=![]() CP,D是CP的中点,将△PAD沿AD折起,使点P到达点P′的位置得到图(二),点M为棱P′C上的动点.
CP,D是CP的中点,将△PAD沿AD折起,使点P到达点P′的位置得到图(二),点M为棱P′C上的动点.
(1)当M在何处时,平面ADM⊥平面P′BC,并证明;
(2)若AB=2,∠P′DC=135°,证明:点C到平面P′AD的距离等于点P′到平面ABCD的距离,并求出该距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 中点M,先证
中点M,先证![]() 与DM,AD垂直,进而证明AD⊥平面D
与DM,AD垂直,进而证明AD⊥平面D![]() C,再证明平面
C,再证明平面![]() BC⊥平面ADM; (2)利用转换顶点三棱锥体积不变底面积相等易证点C到平面
BC⊥平面ADM; (2)利用转换顶点三棱锥体积不变底面积相等易证点C到平面![]() AD的距离等于点
AD的距离等于点![]() 到平面ABCD的距离,并求该距离.
到平面ABCD的距离,并求该距离.
解:(1)当点M为![]() C的中点时,平面ADM⊥平面
C的中点时,平面ADM⊥平面![]() BC,
BC,
证明如下:∵D![]() =DC,M为
=DC,M为![]() C中点,
C中点,
∴![]() C⊥DM,
C⊥DM,
∵AD⊥DP,AD⊥DC,
∴AD⊥平面D![]() C,
C,
∴AD⊥![]() C,
C,
∴![]() C⊥平面ADM,
C⊥平面ADM,
∴平面![]() BC⊥平面ADM;
BC⊥平面ADM;
(2)
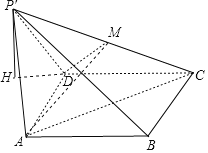
证明:在平面![]() CD上作
CD上作![]() H⊥CD于H,
H⊥CD于H,
由(1)中AD⊥平面D![]() C,
C,
可知平面![]() CD⊥平面ABCD,
CD⊥平面ABCD,
∴![]() H⊥平面ABCD,
H⊥平面ABCD,
由题意得D![]() =2,∠
=2,∠![]() DH=45°,
DH=45°,
∴![]() H=
H=![]() ,
,
又![]() ,
,
设点C到平面![]() AD的距离为h,
AD的距离为h,
即![]() =
=![]() ,
,
由题意△ADC≌△![]() AD,
AD,
∴![]() H=h,
H=h,
故点C到平面![]() AD的距离等于点
AD的距离等于点![]() 到平面ABCD的距离,且距离为
到平面ABCD的距离,且距离为![]() .
.

练习册系列答案
相关题目