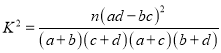题目内容
【题目】在高中学习过程中,同学们经常这样说:“如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
(1)求数学成绩![]() 关于物理成绩
关于物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]() ),若某位学生的物理成绩为80分,预测他的数学成绩;
),若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的五位学生中随机选出三位参加一项知识竞赛,以![]() 表示选中的学生的数学成绩高于100分的人数,求随机变量
表示选中的学生的数学成绩高于100分的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
(参数公式: 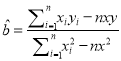 ,
, ![]() .)
.)
参考数据: ![]() ,
,
【答案】(1)![]() ,当
,当![]() 时,
时, ![]() ;
;
(2)所以随机变量![]() 的分布列为
的分布列为
X | 1 | 2 | 3 |
P |
|
|
|
所以![]() .
.
【解析】(【试题分析】(1)依据题设条件线性回归方程的知识求解;(2)借助题设条件运用随机变量的概率分布及随机变量的数学期望公式求解:
1)![]() ,
, ![]() ,
,
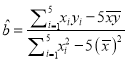
![]() ,
,
![]() ,
,
所以![]() ,当
,当![]() 时,
时, ![]() .
.
(2)随机变量![]() 的可能取值为1,2,3,
的可能取值为1,2,3,
而![]() ,
, ![]() ,
, ![]() ,
,
所以随机变量![]() 的分布列为
的分布列为
X | 1 | 2 | 3 |
P |
|
|
|
所以![]() .
.

【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为![]() .
.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
【题目】某校随机调查了80位学生,以研究学生中爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(Ⅰ)将此样本的频率估计为总体的概率,随机调查了本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列,数学期望及方差;
的分布列,数学期望及方差;
(Ⅱ)根据表中数据,能否有充分证据判断爱好羽毛球运动与性别有关?若有,有多大把握?
| 0.500 | 0.100 | 0.050 | 0.010 |
| 0.455 | 2.706 | 3.841 | 6.635 |
附: