题目内容
(2012•青岛二模)函数y=
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该数列的公比的数是( )
| 9-(x-5)2 |
分析:由题意可知,函数图象为上半圆,根据图象可得圆上点到原点的最短距离为2,最大距离为8.根据等比数列的性质建立方程,可计算出公比的范围,从而判断出结论.
解答: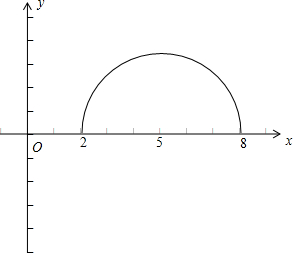 解:函数y=
解:函数y=
等价于
,表示圆心在(5,0),半径为3的上半圆(如图所示),
圆上点到原点的最短距离为2(点2处),最大距离为8(点8处),
若存在三点成等比数列,则最大的公比q应有8=2q2,即q2=4,q=2,
最小的公比应满足2=8q2,所以q2=
,q=
,
所以公比的取值范围为
≤q≤2.
故选D
 解:函数y=
解:函数y=| 9-(x-5)2 |
|
圆上点到原点的最短距离为2(点2处),最大距离为8(点8处),
若存在三点成等比数列,则最大的公比q应有8=2q2,即q2=4,q=2,
最小的公比应满足2=8q2,所以q2=
| 1 |
| 4 |
| 1 |
| 2 |
所以公比的取值范围为
| 1 |
| 2 |
故选D
点评:本题的考点是等比关系的确定,主要考查等比数列的定义,等比中项以及函数作图,属于中档题.

练习册系列答案
相关题目
 (2012•青岛二模)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图示.
(2012•青岛二模)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图示.