题目内容
【题目】已知函数![]() (
(![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() 为整数,
为整数,![]() ,且当
,且当![]() 时,
时,![]() 恒成立,其中
恒成立,其中![]() 为
为![]() 的导函数,求
的导函数,求![]() 的最大值.
的最大值.
【答案】(1)当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;当
;当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;(2)2.
;(2)2.
【解析】
试题分析:(1)求单调增区间,只要解不等式![]() ,它的解集区间就是所求增区间;(2)不等式
,它的解集区间就是所求增区间;(2)不等式![]() 恒成立,不等式具体化为
恒成立,不等式具体化为![]() ,由于
,由于![]() ,因此又可转化为
,因此又可转化为![]() ,这样
,这样![]() 小于
小于![]() 的最小值,因此下面只要求
的最小值,因此下面只要求![]() 的最小值.
的最小值.![]() ,接着要讨论
,接着要讨论![]() 的零点,由于
的零点,由于![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,因此
,因此![]() 在
在![]() 上有唯一零点,即
上有唯一零点,即![]() 在
在![]() 上存在唯一的零点,设其为
上存在唯一的零点,设其为![]() ,则
,则![]() ,可证得
,可证得![]() 为最小值,
为最小值,![]() ,从而整数
,从而整数![]() 的最大值为2.
的最大值为2.
试题解析:(1)![]() .
.
若![]() ,则
,则![]() 恒成立,所以,
恒成立,所以,![]() 在区间
在区间![]() 上单调递增.........2分
上单调递增.........2分
若![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
综上,当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;当
;当![]() 时,
时,![]() 的增区间为
的增区间为![]() ..... 4分
..... 4分
(2)由于![]() ,所以,
,所以,![]()
当![]() 时,
时,![]() ,故
,故![]() ————① 6分
————① 6分
令![]() ,则
,则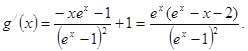
函数![]() 在
在![]() 上单调递增,而
上单调递增,而![]()
所以![]() 在
在![]() 上存在唯一的零点,
上存在唯一的零点,
故![]() 在
在![]() 上存在唯一的零点. 8分
上存在唯一的零点. 8分
设此零点为![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以,![]() 在
在![]() 上的最小值为
上的最小值为![]() .由
.由![]() 可得
可得![]() 10分
10分
所以,![]() 由于①式等价于
由于①式等价于![]() .
.
故整数![]() 的最大值为2. 12分
的最大值为2. 12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:
x | 15.0 | 25.58 | 30.0 | 36.6 | 44.4 |
y | 39.4 | 42.9 | 42.9 | 43.1 | 49.2 |
(1)以x为解释变量,y为预报变量,作出散点图;
(2)求y与x之间的线性回归方程,对于基本苗数56.7预报其有效穗;
(3)计算各组残差,并计算残差平方和;
(4)求R2,并说明残差变量对有效穗的影响占百分之几.


