ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΦΌΕ®–Γ¬σΜυ±ΨΟγ ΐx”κ≥… λΤΎ”––ßΥκy÷°Φδ¥φ‘ΎœύΙΊΙΊœΒΘ§Ϋώ≤βΒΟ5Ήι ΐΨί»γœ¬ΘΚ
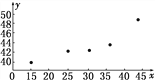
x | 15.0 | 25.58 | 30.0 | 36.6 | 44.4 |
y | 39.4 | 42.9 | 42.9 | 43.1 | 49.2 |
(1)“‘xΈΣΫβ Ά±δΝΩΘ§yΈΣ‘Λ±®±δΝΩΘ§Ής≥ω…ΔΒψΆΦΘΜ
(2)«σy”κx÷°ΦδΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§Ε‘”ΎΜυ±ΨΟγ ΐ56.7‘Λ±®Τδ”––ßΥκΘΜ
(3)ΦΤΥψΗςΉι≤–≤νΘ§≤ΔΦΤΥψ≤–≤νΤΫΖΫΚΆΘΜ
(4)«σR2Θ§≤ΔΥΒΟς≤–≤ν±δΝΩΕ‘”––ßΥκΒΡ”Αœλ’ΦΑΌΖ÷÷°ΦΗΘ°
ΓΨ¥πΑΗΓΩ(1)ΦϊΫβΈω Θ®2Θ©![]() ΘΫ0.29xΘΪ34.708Θ§ΙάΦΤ≥… λΤΎ”––ßΥκ51.151. (3)
ΘΫ0.29xΘΪ34.708Θ§ΙάΦΤ≥… λΤΎ”––ßΥκ51.151. (3) ![]() ΘΫ0.342Θ§
ΘΫ0.342Θ§ ![]() ΘΫ0.773 8Θ§
ΘΫ0.773 8Θ§ ![]() ΘΫΘ≠0.508Θ§
ΘΫΘ≠0.508Θ§ ![]() ΘΫΘ≠2.222Θ§
ΘΫΘ≠2.222Θ§ ![]() ΘΫ1.616.
ΘΫ1.616. ![]() ΘΫ8.521 30.(4) R2ΘΫ0.830Θ§≤–≤ν±δΝΩΙ±œΉΝΥ‘Φ1Θ≠83%ΘΫ17%.
ΘΫ8.521 30.(4) R2ΘΫ0.830Θ§≤–≤ν±δΝΩΙ±œΉΝΥ‘Φ1Θ≠83%ΘΫ17%.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ(1)Ϋ®ΝΔΉχ±ξœΒΗυΨίΗςΉι÷ΒΒψ≥ωΟΩΗωΒψΦ¥Ω…Θ®2Θ©”…ΆΦΩ¥≥ωΘ§―υ±ΨΒψ≥ ΧθΉ¥Ζ÷≤ΦΘ§”–±»ΫœΚΟΒΡœΏ–‘œύΙΊΙΊœΒΘ§“ρ¥ΥΩ…“‘”ΟœΏ–‘ΜΊΙιΖΫ≥ΧΩΧΜ≠ΥϋΟ«÷°ΦδΒΡΙΊœΒΘ§ΗυΨί±μ÷– ΐΨίΘ§ΦΤΥψ![]() Θ§
Θ§ ![]() ”κ
”κ![]() –¥≥ωœΏ–‘ΜΊΙιΖΫ≥ΧΘ§¥ζ»κxΘΫ56.7 ±Φ¥ΒΟΫβΘ®3Θ©”…”ΎyΘΫbxΘΪaΘΪeΘ§Ω…“‘ΥψΒΟ
–¥≥ωœΏ–‘ΜΊΙιΖΫ≥ΧΘ§¥ζ»κxΘΫ56.7 ±Φ¥ΒΟΫβΘ®3Θ©”…”ΎyΘΫbxΘΪaΘΪeΘ§Ω…“‘ΥψΒΟ![]() ΘΫyiΘ≠
ΘΫyiΘ≠![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΘΫ0.342Θ§
ΘΫ0.342Θ§ ![]() ΘΫ0.773 8Θ§
ΘΫ0.773 8Θ§ ![]() ΘΫΘ≠0.508Θ§
ΘΫΘ≠0.508Θ§ ![]() ΘΫΘ≠2.222Θ§
ΘΫΘ≠2.222Θ§ ![]() ΘΫ1.616.Ϋχ––«σΚΆΦ¥ΒΟΉή≤–≤νΤΫΖΫΚΆΘ®4Θ©ΦΤΥψΉήΤΪ≤νΤΫΖΫΚΆΘ§ΜΊΙιΤΫΖΫΚΆ=ΉήΤΪ≤νΤΫΖΫΚΆ-≤–≤νΤΫΖΫΚΆΘ§¥ζ»κΙΪ ΫΒΟR2Θ§Ϋβ Ά±δΝΩ–Γ¬σΜυ±ΨΟγ ΐΕ‘Ήή–ß”ΠΙ±œΉΦ¥ΒΟΘ§≤–≤ν±δΝΩΙ±œΉΦ¥ΒΟ.
ΘΫ1.616.Ϋχ––«σΚΆΦ¥ΒΟΉή≤–≤νΤΫΖΫΚΆΘ®4Θ©ΦΤΥψΉήΤΪ≤νΤΫΖΫΚΆΘ§ΜΊΙιΤΫΖΫΚΆ=ΉήΤΪ≤νΤΫΖΫΚΆ-≤–≤νΤΫΖΫΚΆΘ§¥ζ»κΙΪ ΫΒΟR2Θ§Ϋβ Ά±δΝΩ–Γ¬σΜυ±ΨΟγ ΐΕ‘Ήή–ß”ΠΙ±œΉΦ¥ΒΟΘ§≤–≤ν±δΝΩΙ±œΉΦ¥ΒΟ.
‘ΧβΫβΈωΘΚ
(1)»γœ¬ΆΦΥυ ΨΘΚ
(2)”…ΆΦΩ¥≥ωΘ§―υ±ΨΒψ≥ ΧθΉ¥Ζ÷≤ΦΘ§”–±»ΫœΚΟΒΡœΏ–‘œύΙΊΙΊœΒΘ§“ρ¥ΥΩ…“‘”ΟœΏ–‘ΜΊΙιΖΫ≥ΧΩΧΜ≠ΥϋΟ«÷°ΦδΒΡΙΊœΒΘ°…ηΜΊΙιΖΫ≥ΧΈΣ![]() ΘΫ
ΘΫ![]() xΘΪ
xΘΪ![]() Θ§
Θ§![]() ΘΫ30.316Θ§
ΘΫ30.316Θ§![]() ΘΫ43.5Θ§
ΘΫ43.5Θ§![]() ΘΫ5 090.256 4Θ§
ΘΫ5 090.256 4Θ§
![]() ΓΓ
ΓΓ![]() ΘΫ1 318.746Θ§
ΘΫ1 318.746Θ§![]() 2ΘΫ1 892.25Θ§
2ΘΫ1 892.25Θ§![]() 2ΘΫ919.059 9Θ§
2ΘΫ919.059 9Θ§
![]() iyiΘΫ6 737.322.
iyiΘΫ6 737.322.
‘ρ![]() ΘΫ
ΘΫ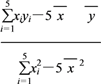 Γ÷0.29.
Γ÷0.29.![]() ΘΫ
ΘΫ![]() Θ≠
Θ≠![]()
![]() Γ÷34.708.
Γ÷34.708.
Ι Υυ«σΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ![]() ΘΫ0.29xΘΪ34.708.
ΘΫ0.29xΘΪ34.708.
Β±xΘΫ56.7 ±Θ§![]() ΘΫ0.29ΓΝ56.7ΘΪ34.708ΘΫ51.151Θ§ΙάΦΤ≥… λΤΎ”––ßΥκ51.151.
ΘΫ0.29ΓΝ56.7ΘΪ34.708ΘΫ51.151Θ§ΙάΦΤ≥… λΤΎ”––ßΥκ51.151.
(3)”…”ΎyΘΫbxΘΪaΘΪeΘ§Ω…“‘ΥψΒΟ![]() iΘΫyiΘ≠
iΘΫyiΘ≠![]() iΖ÷±πΈΣ
iΖ÷±πΈΣ![]() ΘΫ0.342Θ§
ΘΫ0.342Θ§ ![]() ΘΫ0.773 8Θ§
ΘΫ0.773 8Θ§ ![]() ΘΫΘ≠0.508Θ§
ΘΫΘ≠0.508Θ§ ![]() ΘΫΘ≠2.222Θ§
ΘΫΘ≠2.222Θ§ ![]() ΘΫ1.616.
ΘΫ1.616.
≤–≤νΤΫΖΫΚΆΘΚ![]() ΘΫ8.521 30.
ΘΫ8.521 30.
(4)ΉήΤΪ≤νΤΫΖΫΚΆΘΚ![]() (yiΘ≠
(yiΘ≠![]() )2ΘΫ50.18Θ§
)2ΘΫ50.18Θ§
ΜΊΙιΤΫΖΫΚΆΘΚ50.18Θ≠8.521 30ΘΫ41.658 7Θ§
R2ΘΫ0.830.
ΓύΫβ Ά±δΝΩ–Γ¬σΜυ±ΨΟγ ΐΕ‘Ήή–ß”ΠΙ±œΉΝΥ‘Φ83%.
≤–≤ν±δΝΩΙ±œΉΝΥ‘Φ1Θ≠83%ΘΫ17%.