题目内容
(本小题满分14分)
如图所示,四棱锥 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,
,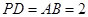 ,
, ,
, ,
, 分别为
分别为 、
、 、
、 的中点.
的中点.

(1)求证: ;
;
(2)求平面EFG与平面ABCD所成锐二面角的余弦值.
如图所示,四棱锥
 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,
,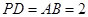 ,
, ,
, ,
, 分别为
分别为 、
、 、
、 的中点.
的中点.
(1)求证:
 ;
;(2)求平面EFG与平面ABCD所成锐二面角的余弦值.
(1)要证  ,只需证
,只需证 ,只需证
,只需证  平面
平面 ; (2)
; (2) 。
。
 ,只需证
,只需证 ,只需证
,只需证  平面
平面 ; (2)
; (2) 。
。试题分析:(1)∵
 平面
平面 ,
, 平面
平面 ,
,∴
 又
又 为正方形,∴
为正方形,∴ .又
.又 ,…………3分
,…………3分∴
 平面
平面 ∵
∵ 平面
平面 ,∴
,∴ . ………………………………5分
. ………………………………5分∵
 中,中位线
中,中位线 ,∴
,∴ ……………6分
……………6分(2)记AD中点为H,连结FH、HG,易知GH//DC,
 ,
, 又
 中EF//DC,∴EF//GH所以E、F、H、G四点共面……7分
中EF//DC,∴EF//GH所以E、F、H、G四点共面……7分∴平面EFG与平面ABCD交于GH,所求锐二面角为F-GH-D.……………8分
由(1)
 平面
平面 ,EF//DC//GH∴
,EF//DC//GH∴ 平面
平面
即
 平面FHD,
平面FHD, 平面FHD,
平面FHD,所以
 FH,
FH, DH,
DH,∴二面角F-GH-D的平面角是
 ……………………11分
……………………11分FH是等腰直角
 的中位线,
的中位线, =
= …………………………13分
…………………………13分 ∴所求锐二面角的余弦值为
∴所求锐二面角的余弦值为 .………………14分
.………………14分证法2:DA、DC、DP两两垂直,以
 为原点建立空间直角坐标系
为原点建立空间直角坐标系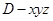 …1分
…1分
则
 ,
, ,
, ,
, ,G(1,2,0), ………3分
,G(1,2,0), ………3分(1)
 ,
, ………………4分
………………4分∵
 ∴
∴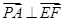 ……6分
……6分∴
 ………………………………………7分
………………………………………7分(2)∵
 平面
平面 ,
,∴
 是平面
是平面 的一个法向量.………9分
的一个法向量.………9分设平面EFG的法向量为
 ,∵
,∵
 令
令 ,得
,得 是平面
是平面 的一个法向量. …………11分
的一个法向量. …………11分∵
 …………………………13分
…………………………13分∴所求锐二面角的余弦值为
 . ……………………………14分
. ……………………………14分点评:二面角的求法是立体几何中的一个难点。我们解决此类问题常用的方法有两种:①综合法,综合法的一般步骤是:一作二说三求。②向量法,运用向量法求二面角应注意的是计算。很多同学都会应用向量法求二面角,但结果往往求不对,出现的问题就是计算错误。

练习册系列答案
相关题目
 点
点 上,过点
上,过点 做
做 //
// 将
将 的位置(
的位置( ),
), .
.
 (II)试问:当点
(II)试问:当点 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.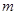 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题中不正确的是( )
是两个不同的平面,则下列命题中不正确的是( )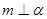 ,则
,则


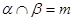 ,
,
 ,
, ,
, ,
,

 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.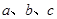 及平面
及平面 ,它们具备下列哪组条件时,有
,它们具备下列哪组条件时,有 成立( )
成立( )

 和
和
 ⊥平面
⊥平面 ,直线m
,直线m 平面
平面 ,有下列命题:
,有下列命题: ∥
∥
 ∥m;
∥m; 中,
中, 、
、 分别是
分别是 、
、 的中点,则异面直线
的中点,则异面直线 与
与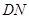 所成的角的大小是____________.
所成的角的大小是____________.
 的中线AF与中位线DE相交于G,已知
的中线AF与中位线DE相交于G,已知 是
是 绕边DE旋转过程中的一个图形,给出四个命题:
绕边DE旋转过程中的一个图形,给出四个命题: 在
在 上的射影在线段
上的射影在线段 上;
上; ;
;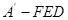 的体积有最大值;
的体积有最大值; 与
与 不可能垂直.
不可能垂直.
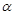 与平面
与平面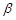 相交,那么平面
相交,那么平面