题目内容
19.已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A(-2,0),B(2,0),离心率e=$\frac{\sqrt{3}}{2}$.(1)求椭圆M的方程;
(2)若F1,F2是椭圆M的左,右焦点,以线段F1F2为直径作圆N,点C(C点不同于F1,F2,且不在y轴上)为圆N上任一点,直线F1C与直线x=$\sqrt{3}$交于点R,D为线段RF2的中点,试判断直线CD与圆N的位置关系,并证明你的结论.
分析 (1)由题意可得a=2,运用离心率公式可得c,由a,b,c的关系可得b=1,进而得到椭圆方程;
(2)求出焦点坐标,求得圆N的半径,可得圆的方程,求出直线CD的斜率,以及直线OC的斜率,证明它们互为负倒数,即可得证.
解答 解:(1)由题意可得a=2,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,所以c=$\sqrt{3}$,从而b2=a2-c2=1.
所以椭圆M方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)椭圆M的焦点为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),
圆N的圆心在原点,半径为r=$\sqrt{3}$,
所以圆N的方程为x2+y2=3.
设C(m,n)(m≠0,n≠0),点R的坐标为($\sqrt{3}$,t),
因为F1、C、R三点共线,所以$\overrightarrow{{F}_{1}C}$∥$\overrightarrow{{F}_{1}R}$,而$\overrightarrow{{F}_{1}C}$=(m+$\sqrt{3}$,n),$\overrightarrow{{F}_{1}R}$=(2$\sqrt{3}$,t),
所以2$\sqrt{3}$n=t(m+$\sqrt{3}$),即t=$\frac{2\sqrt{3}n}{m+\sqrt{3}}$,
所以点R的坐标为($\sqrt{3}$,$\frac{2\sqrt{3}n}{m+\sqrt{3}}$),点D的坐标为($\sqrt{3}$,$\frac{\sqrt{3}n}{m+\sqrt{3}}$),
所以直线CD的斜率为k=$\frac{n-\frac{\sqrt{3}n}{m+\sqrt{3}}}{m-\sqrt{3}}$=$\frac{(m+\sqrt{3})n-\sqrt{3}n}{{m}^{2}-3}$=$\frac{mn}{{m}^{2}-3}$.
因为m2+n2=3,所以m2-3=-n2,所以k=$\frac{mn}{-{n}^{2}}$=-$\frac{m}{n}$,
又直线OC(O为坐标原点)的斜率为kOC=$\frac{n}{m}$,
所以kOC•k=-1,所以直线CD⊥OC.
所以直线CD与圆N相切.
点评 本题考查椭圆方程的求法,注意运用离心率公式,考查直线与圆的位置关系的判断,注意运用直线的斜率公式,考查运算能力,属于中档题.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案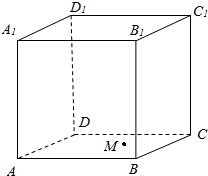 如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |