题目内容
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() .已知以
.已知以![]() 为圆心,半径为4的圆与
为圆心,半径为4的圆与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 是该圆与抛物线
是该圆与抛物线![]() 的一个交点,
的一个交点,![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() 的纵坐标为
的纵坐标为![]() 且在
且在![]() 上,
上,![]() 、
、![]() 是
是![]() 上异于点
上异于点![]() 的另两点,且满足直线
的另两点,且满足直线![]() 和直线
和直线![]() 的斜率之和为
的斜率之和为![]() ,试问直线
,试问直线![]() 是否经过一定点,若是,求出定点的坐标,否则,请说明理由.
是否经过一定点,若是,求出定点的坐标,否则,请说明理由.
【答案】(1)2.(2)![]() .
.
【解析】
试题分析:1)由题意及抛物线定义,![]() 为边长为4的正三角形,
为边长为4的正三角形,![]() ,
,![]() 。(2)设直线
。(2)设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,
,![]() .由点差法得
.由点差法得![]() ,结合韦达,得到m与t的关系,代入直线方程可求到定点。
,结合韦达,得到m与t的关系,代入直线方程可求到定点。
试题解析:(1)由题意及抛物线定义,![]() ,
,![]() 为边长为4的正三角形,设准线
为边长为4的正三角形,设准线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,
,![]() .
.
由![]() ,得
,得![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
又点![]() 在抛物线
在抛物线![]() 上,则
上,则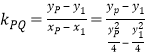
![]() ,同理可得
,同理可得![]() .
.
因为![]() ,所以
,所以![]()
![]()
![]() ,解得
,解得![]() .
.
由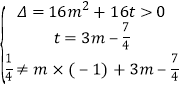 ,解得
,解得![]() .
.
所以直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目
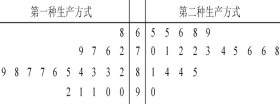
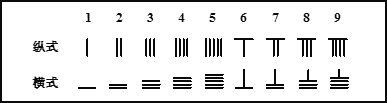
【题目】随着全民健康运动的普及,每天一万步已经成为一种健康时尚,某学校为了教职工健康工作,在全校范围内倡导“每天一万步”健步走活动,学校界定一人一天走路不足4千步为健步常人,不少于16千步为健步超人,其他为健步达人,学校随机抽查了36名教职工,其每天的走步情况统计如下:
步数 |
|
|
|
人数 | 6 | 18 | 12 |
现对抽查的36人采用分层抽样的方式选出6人
(1)求从这三类人中各抽多少人;
(2)现从选出的6人中随机抽取2人,求这两人健步类型相同的概率.