题目内容
某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩分组如下:第一组[65,70),第二组 [70,75),第三组[75,80),第四组 [80,85),第五组 [85,90)(假设考试成绩均在[65,90)内),得到频率分布直方图如图: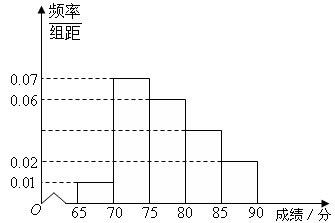
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的的概率.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由所有频率的和为 ,易得测试成绩在[80,85)内的频率;(2)先分别求出第三组、第四组、第五组的人数,再由分层抽样方法得各组应该抽取的人数。用字母表示所研究的事件,用列举法得基本事件的总数以及所研究事件含多少个基本事件,最后利用古典概型公式求得概率.
,易得测试成绩在[80,85)内的频率;(2)先分别求出第三组、第四组、第五组的人数,再由分层抽样方法得各组应该抽取的人数。用字母表示所研究的事件,用列举法得基本事件的总数以及所研究事件含多少个基本事件,最后利用古典概型公式求得概率.
试题解析:(1)测试成绩在[80,85)内的频率为: 2分
2分 3分
3分
(2)第三组的人数等于 ,第四组的人数等于
,第四组的人数等于 ,
,
第五组的人数等于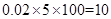 , 5分
, 5分
分组抽样各组的人数为第三组3人,第四组2人,第五组1人. 6分
设第三组抽到的3人为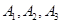 ,第四组抽到的2人为
,第四组抽到的2人为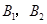 ,第五组抽到的1人为
,第五组抽到的1人为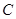 . 7分
. 7分
这6名同学中随机选取2名的可能情况有15种,如下: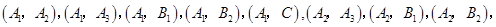
 . 10分
. 10分
设“第四组2名同学至少有一名同学被抽中”为事件 ,事件
,事件 包含的事件个数有9种,即:
包含的事件个数有9种,即:

 ,
, ,
, ,
,
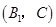 ,
,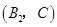 . 11分
. 11分
所以, 事件 的概率即第四组至少有一名同学被抽中的概率为
的概率即第四组至少有一名同学被抽中的概率为 . 12分
. 12分
考点:1、考查频率分布;2、频率分布直方图;3、古典概型.

 字词句段篇系列答案
字词句段篇系列答案甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为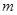 ,
,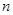 (
(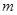 >
>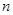 ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
 |  | 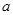 |  |  |
(Ⅱ)求
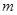 ,
,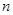 的值;
的值;(Ⅲ)求
 的数学期望.
的数学期望. 为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 | 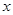 |
| B | 12 | 3 |
| C | 8 |  |
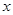 与
与 的值;
的值;(2)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
根据以往资料统计,大学生购买某品牌平板电脑时计划采用分期付款的期数ζ的分布列为
| ζ | 1 | 2 | 3 |
| P | 0.4 | 0.25 | 0.35 |
(2)若签订协议后,在实际付款中,采用1期付款的没有变化,采用2、3期付款的都至多有一次改付款期数的机会,其中采用2期付款的只能改为3期,概率为
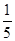 ;采用3期付款的只能改为2期,概率为
;采用3期付款的只能改为2期,概率为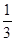 .数码城销售一台该平板电脑,实际付款期数
.数码城销售一台该平板电脑,实际付款期数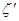 与利润
与利润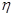 (元)的关系为
(元)的关系为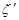 | 1 | 2 | 3 |
| η | 200 | 250 | 300 |
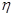 的分布列及期望E(
的分布列及期望E(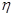 ).
).  ,家长所得点数记为
,家长所得点数记为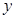 ;
; ,家长的计算器产生的随机实数记为
,家长的计算器产生的随机实数记为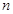 .
.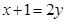 ,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率; ,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率. 只,其中有
只,其中有 只合格品,
只合格品, 只次品。
只次品。 次,每次取一只灯泡,求
次,每次取一只灯泡,求 的分布列和数学期望.
的分布列和数学期望.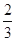 .
.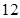 个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得
个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得 分,选对得
分,选对得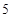 分.在这次考试的选择题部分,某考生比较熟悉其中的
分.在这次考试的选择题部分,某考生比较熟悉其中的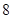 个题,该考生做对了这
个题,该考生做对了这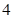 个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题:
个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题: 分的概率;
分的概率; ,求
,求