题目内容
根据以往资料统计,大学生购买某品牌平板电脑时计划采用分期付款的期数ζ的分布列为
| ζ | 1 | 2 | 3 |
| P | 0.4 | 0.25 | 0.35 |
(2)若签订协议后,在实际付款中,采用1期付款的没有变化,采用2、3期付款的都至多有一次改付款期数的机会,其中采用2期付款的只能改为3期,概率为
 ;采用3期付款的只能改为2期,概率为
;采用3期付款的只能改为2期,概率为 .数码城销售一台该平板电脑,实际付款期数
.数码城销售一台该平板电脑,实际付款期数 与利润
与利润 (元)的关系为
(元)的关系为 | 1 | 2 | 3 |
| η | 200 | 250 | 300 |
 的分布列及期望E(
的分布列及期望E( ).
).
(1) .
.
(2) 的分布列为
的分布列为
200 250 300 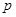
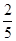


 的期望
的期望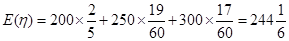 (元).
(元).
解析试题分析:(1)若事件 ={购买该平板电脑的3位大学生中,至少有1位采用1期付款},则事件
={购买该平板电脑的3位大学生中,至少有1位采用1期付款},则事件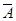 ={购买该平板电脑的3位大学生中没有1位采用1期付款}.
={购买该平板电脑的3位大学生中没有1位采用1期付款}.
∵ , 2分
, 2分
∴ . 4分
. 4分
(2)根据题意,实际付款期数 的概率为
的概率为 ,
, ,
,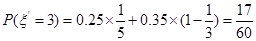 , 10分
, 10分
而销售一台该平板电脑的利润 的可能值为200元,250元,300元. 11分
的可能值为200元,250元,300元. 11分
∴ ,
, ,
,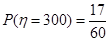 ,
,
∴ 的分布列为
的分布列为
12分
200 250 300 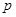
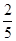


∴ 的期望
的期望 (元).14分
(元).14分
考点:对立事件的概率计算,随机变量的分布列及数学期望。
点评:中档题,随机变量的分布列及其数学期望的确定,关键是概率的计算,除直接套用公式计算的外,要注意理解变量取值的意义,准确的进行概率计算。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.

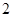 个白球和
个白球和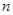 个红球
个红球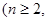 且
且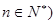 ,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.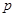 ;
;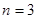 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;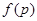 ,当
,当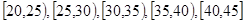 .
.  的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在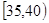 岁的人数;
岁的人数;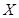 ,求
,求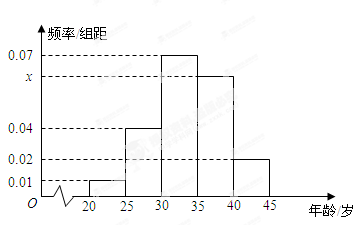

 是从
是从 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 四个数中任取的一个数,求
四个数中任取的一个数,求 为偶函数的概率;
为偶函数的概率; ,
, 任取的一个数,求方程
任取的一个数,求方程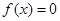 有实根的概率.
有实根的概率.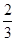 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.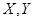 ,求
,求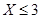 的概率;
的概率; 局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是
局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是 。假设各局比赛结果相互独立。
。假设各局比赛结果相互独立。 胜利的概率;
胜利的概率; 或
或 ,则胜利方得
,则胜利方得 分;若比赛结果为
分;若比赛结果为 ,则胜利方得
,则胜利方得 分、对方得
分、对方得 分。求乙队得分
分。求乙队得分 的分布列及数学期望。
的分布列及数学期望。