Question

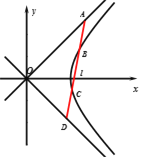
【题目】已知双曲线，不与轴垂直的直线与双曲线右支交于点，，（在轴上方，在轴下方），与双曲线渐近线交于点，（在轴上方），为坐标原点，下列选项中正确的为（ ）

A.恒成立

B.若，则

C.面积的最小值为1

D.对每一个确定的，若，则的面积为定值

Answer 1

【答案】ABD

【解析】

对于A选项，设直线方程为，分别与双曲线方程以及双曲线的渐近线方程联立，求出中点坐标，并判断是否相等即可；对于B选项，由，得到，结合A选项的结果，即可判断选项B是否正确；对于C选项，设直线方程为，，直线分别与渐近线方程联立，求出坐标，进而求出的面积，根据的范围，求出的面积的范围即可；对于D选项，由已知可得，利用选项A的方程，得到关系，求出的面积即可.

设，代入得，①

显然，，即，

设，，则，是方程①的两个根，

有，，

设，，由得，

由，得；

所以，所以和的中点重合，

所以，所以恒成立．故A正确．

因为和的中点重合为，所以，

又，所以，

所以，故B正确．

设直线方程为，，

由得，由得，

，，，

，故C错误.

因为，所以，得

，即，

所以，，又，，，

所以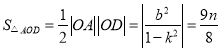是定值．故D正确．

故选：ABD.