题目内容
【题目】已知数列{an}满足:a1=0,![]() (n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
(n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
A.![]() 是单调递增数列,
是单调递增数列,![]() 是单调递减数列B.
是单调递减数列B.![]()
C.![]() D.
D.![]()
【答案】C
【解析】
设![]() ,则有
,则有![]() ,
,![]() ,构建
,构建![]() ,求导分析可知导函数恒大于零,即数列
,求导分析可知导函数恒大于零,即数列![]() 都是单调数列,分别判定
都是单调数列,分别判定![]() ,即得单调性,数列
,即得单调性,数列![]() 与数列
与数列![]() 的单调性一致,可判定A选项正确;B、C选项利用分析法证明,可知B正确,C错误;D选项利用数学归纳法证分两边证
的单调性一致,可判定A选项正确;B、C选项利用分析法证明,可知B正确,C错误;D选项利用数学归纳法证分两边证![]() ,即可证得
,即可证得![]() .
.
由题可知,a1=0,![]() ,
,![]()
设![]() ,则有
,则有![]() ,即
,即![]()
令![]() ,则
,则![]() ,这里将
,这里将![]() 视为
视为![]() 上的前后两点,因函数
上的前后两点,因函数![]() 单调递增,所以
单调递增,所以![]() ,
,
所以数列![]() 都是单调数列
都是单调数列
又因为![]() 同理可知,
同理可知,![]() ,所以
,所以![]() 单调递增,
单调递增,![]() 单调递减
单调递减
因为数列![]() 与数列
与数列![]() 的单调性一致,所以
的单调性一致,所以![]() 单调递增,
单调递增,![]() 单调递减,
单调递减,
故A选项正确;
因为![]() ,则
,则![]() ,欲证
,欲证![]() ,即
,即![]()
由![]() ,上式化为
,上式化为![]() ,
,
显然![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,故
,故![]() 成立;
成立;
所以原不等式成立
故B选项正确;
欲证![]() ,只需证
,只需证![]() ,即
,即![]()
即![]() ,显然成立
,显然成立
故![]() ,所以
,所以![]()
故C选项错误;
欲证![]() ,因单调性一致则只需证
,因单调性一致则只需证![]() ,只需证
,只需证![]()
因为![]() ,若
,若![]() ,则
,则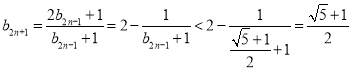 ;
;
又因为![]() ,若
,若![]() ,则
,则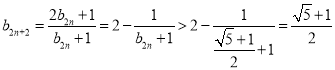 ;
;
由数学归纳法有![]() ,则
,则![]() 成立
成立
故D选项正确。
故答案为:C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目