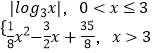题目内容
【题目】设函数 ![]() 的定义域为
的定义域为 ![]() ,值域为
,值域为 ![]() ,如果存在函数
,如果存在函数 ![]() ,使得函数
,使得函数 ![]() 的值域仍是
的值域仍是 ![]() ,那么称
,那么称 ![]() 是函数
是函数 ![]() 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数 ![]() 是不是函数
是不是函数 ![]() 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;
① ![]() ;
;
② ![]() .
.
(2)设 ![]() 的定义域为
的定义域为 ![]() ,已知
,已知 ![]() 是
是 ![]() 的一个等值域变换,且函数
的一个等值域变换,且函数 ![]() 的定义域为
的定义域为 ![]() ,求实数
,求实数 ![]() 的值.
的值.
【答案】
(1)解:① ![]() ,x>0,值域为R ,
,x>0,值域为R , ![]() ,t>0,由g(t)2可得y=f[g(t)]的值域为[1,+∞).
,t>0,由g(t)2可得y=f[g(t)]的值域为[1,+∞).
则x=g(t)不是函数y=f(x)的一个等值域变换;
② ![]() ,即
,即 ![]() 的值域为
的值域为 ![]() ,
,
当 ![]() 时,
时, ![]() ,即
,即 ![]() 的值域仍为
的值域仍为 ![]() ,所以
,所以 ![]() 是
是 ![]() 的一个等值域变换,故①不是等值域变换,②是等值域变换;
的一个等值域变换,故①不是等值域变换,②是等值域变换;
(2)解: ![]() 定义域为
定义域为 ![]() ,因为
,因为 ![]() 是
是 ![]() 的一个等值域变换,且函数
的一个等值域变换,且函数 ![]() 的定义域为
的定义域为 ![]() ,
, ![]() 的值域为
的值域为 ![]() ,
,![]() ,
,![]() 恒有
恒有 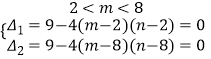 ,解得
,解得 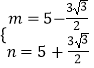 .
.
【解析】(1)在①中,函数 f ( x )的值域为R,函数y=f[g(t)]的值域为[1,+∞).所以①不是一个等值域变换。在②中f ( x ) 的值域为 [![]() , + ∞ ),y = f [ g ( t ) ] 的值域仍为 [,
, + ∞ ),y = f [ g ( t ) ] 的值域仍为 [,![]() , + ∞ ),所以①不是等值域变换,②是等值域变换。
, + ∞ ),所以①不是等值域变换,②是等值域变换。
(2)由题意可以得x = g ( t ) = ![]() , t ∈ R 的值域为 [ 2 , 8 ],通过2≤
, t ∈ R 的值域为 [ 2 , 8 ],通过2≤![]() ≤8 2 ( t 2 + 1 ) ≤ m t 2 3 t + n ≤ 8 ( t 2 + 1 ),可以求出m、n的值。
≤8 2 ( t 2 + 1 ) ≤ m t 2 3 t + n ≤ 8 ( t 2 + 1 ),可以求出m、n的值。
【考点精析】利用函数的定义域及其求法和函数的值域对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.

 名校课堂系列答案
名校课堂系列答案