题目内容
【题目】已知函数 
的部分图象如图所示．
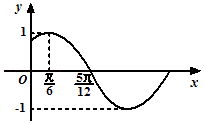
（1）求函数f（x）的解析式；
（2）在△ABC中，角A，B，C的对边分别是a，b，c，若（2a﹣c）cosB=bcosC，求 
的取值范围．
【答案】
（1）
解：由图象知A=1， 
，∴ω=2，
∴f（x）=sin（2x+φ）
∵图象过（ 
），将点（ ）代入解析式得 
，
∵ 
，
∴ 
故得函数 
（2）
解：由（2a﹣c）cosB=bcosC，
根据正弦定理，得：（2sinA﹣sinC）cosB=sinBcosC
∴2sinAcosB=sin（B+C），
∴2sinAcosB=sinA．
∵A∈（0，π），
∴sinA≠0，
∴cosB= 
，即B= 
∴A+C= 
，即 
那么： 
，
故得 
【解析】（1）根据图象求出A，ω 和φ，即可求函数f（x）的解析式；（2）利用正弦定理化简，求出B，根据三角内角定理可得A的范围，利用函数解析式之间的关系即可得到结论
练习册系列答案
相关题目
【题目】现有1 000根某品种的棉花纤维，从中随机抽取50根，纤维长度（单位：mm）的数据分组及各组的频数见右上表，据此估计这1 000根中纤维长度不小于37.5 mm的根数是 ．
纤维长度 | 频数 |
[22.5，25.5) | 3 |
[25.5，28.5) | 8 |
[28.5，31.5) | 9 |
[31.5，34.5) | 11 |
[34.5，37.5) | 10 |
[37.5，40.5) | 5 |
[40.5，43.5] | 4 |
