题目内容
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= ![]() PD.
PD.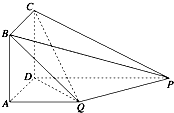
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q﹣BP﹣C的正弦值.
【答案】
(1)
解:由题意可得QA⊥平面ABCD,∴QA⊥CD.
由四边形ABCD为正方形知DC⊥AD,又QA、AD为平面PDAQ内
两条相交直线,
∴CD⊥平面PDAQ,∴CD⊥PQ.
在直角梯形PDAQ中可得DQ=PQ= ![]() PD,
PD,
∴PQ2+DQ2=PD2.
由勾股定理得逆定理得:PQ⊥QD.
又CD、QD为平面ADCB内两条相交直线,
∴PQ⊥平面DCQ.
再由PQ平面PQC,可得平面PQC⊥平面DCQ
(2)
解:
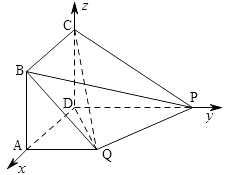
如图,以D为坐标原点,线段DA的长为单位长,
射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz;
依题意有Q(1,1,0),C(0,0,1),P(0,2,0),B(1,0,1),
![]() =(1,0,0),
=(1,0,0), ![]() =(﹣1,2,﹣1).
=(﹣1,2,﹣1).
设 ![]() =(x,y,z)是平面的PBC法向量,则
=(x,y,z)是平面的PBC法向量,则 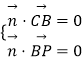 ,即
,即 ![]() ,
,
可取 ![]() =( 0,﹣1,﹣2).
=( 0,﹣1,﹣2).
同理求得平面PBQ的法向量 ![]() =(1,1,1).
=(1,1,1).
所以cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =﹣
=﹣ ![]() ,故有 sin<
,故有 sin< ![]() ,
, ![]() >=
>= ![]() ,
,
即二面角Q﹣BP﹣C的正弦值为 ![]() .
.
【解析】(1)先证明CD⊥平面PDAQ,可得CD⊥PQ;再由勾股定理得逆定理证得PQ⊥QD.再利用直线和平面垂直的判定定理证得PQ⊥平面DCQ,从而证得平面PQC⊥平面DCQ.(2)如图建立空间坐标系,求得 ![]() 和
和 ![]() 的坐标,再求得平面的PBC法向量
的坐标,再求得平面的PBC法向量 ![]() 的坐标,同理求得平面PBQ的法向量
的坐标,同理求得平面PBQ的法向量 ![]() 的坐标,求得cos<
的坐标,求得cos< ![]() ,
, ![]() >=
>= ![]() 的值,从而求得sin<
的值,从而求得sin< ![]() ,
, ![]() >的值,即为所求.
>的值,即为所求.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案