题目内容
已知△ABC的面积S满足3≤S≤3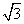 ,且
,且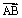 ·
·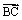 =6,
=6,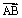 与
与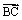 的夹角为
的夹角为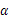
(1)求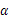 的取值范围;
的取值范围;
(2)若函数f(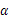 )=sin2
)=sin2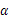 +2sin
+2sin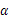 cos
cos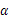 +3cos2
+3cos2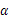 ,求f(
,求f(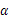 )的最小值.
)的最小值.
【答案】
解:(1)由题意知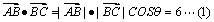
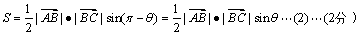
由②÷①得=tanθ即3tanθ=S……(3分)?
由3≤S≤3得3≤3tanθ≤3……(4分)?
又θ为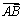 与
与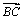 的夹角,∴θ∈〔0,π〕∴θ∈〔,〕……(6分)
的夹角,∴θ∈〔0,π〕∴θ∈〔,〕……(6分)
(2)f(θ)=sin2θ+2sinθcosθ+3cos2θ=1+sin2θ+2cos2θ?
∴f(θ)=2+sin2θ+cos2θ=2+sin(2θ+)……(9分)?
∵θ∈〔,〕,∴2θ+∈〔, 〕?
∴2θ+=,即θ=时,f(θ) min=……(12分)

练习册系列答案
相关题目