题目内容
某校高三年级举行的一次演讲
比赛共有10位同学参加,其中一班有3位,二班有2位,其他 班有5位．若采取抽
签的方式确定他们的演讲顺序，则一班的3位同学恰好被排在一起 （指演讲序号相连），而二班的2位同学没有被排在一起的概率为（ ）
比赛共有10位同学参加,其中一班有3位,二班有2位,其他 班有5位．若采取抽签的方式确定他们的演讲顺序，则一班的3位同学恰好被排在一起 （指演讲序号相连），而二班的2位同学没有被排在一起的概率为（ ）A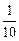． | B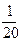． | C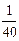． | D． |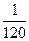
B
解：10位同学总参赛次序A
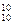．一班3位同学恰好排在一起,而二班的2位同学没有排在一起的方法数为先将一班3人捆在一起A
,与另外5人全排列A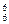
,二班2位同学不排在一起,采用插空法A
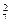,即A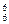AA．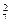
∴所求概率为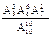
= 
．
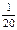故选B
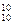总参赛次序A．一班3位同学恰好排在一起,而二班的2位同学没有排在一起的方法数为先将一班3人捆在一起A,与另外5人全排列A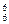,二班2位同学不排在一起,采用插空法A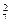,即A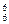AA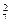．∴所求概率为
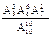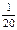= ．故选B
练习册系列答案
阅读快车系列答案
相关题目
．
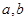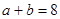”的概率；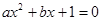
有实根”的概率．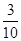
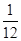
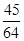
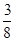
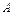至少发生一次的概率为
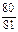，则在一次试验中事件
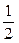
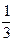
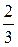
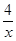，P(B)＝
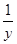，则x＋y的最小值为( )
。这三项测试能否通过相互之间没有影响。