题目内容
已知双曲线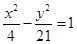 ,
,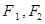 分别为它的左、右焦点,
分别为它的左、右焦点,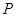 为双曲线上一点,
为双曲线上一点,
且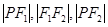 成等差数列,则
成等差数列,则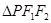 的面积为 .
的面积为 .

解析试题分析:不妨设P为双曲线右支上一点,则|PF1|-|PF2|=4………………①
又|PF1|,|F1F2|,|PF2|成等差数列,|F1F2|=10,所以|PF1|+|PF2|=20………………②
由①②可得|PF1|=12,|PF2|=8.所以由余弦定理得:cos∠F1PF2=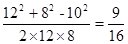 ,
,
所以sin∠F1PF2=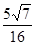 ,所以
,所以 =|PF1||PF2|sin∠F1PF2=
=|PF1||PF2|sin∠F1PF2= 。
。
考点:双曲线的简单性质;等差中项的定义;三角形的面积公式。
点评:本题主要考查了等差数列的性质、双曲线的定义和余弦定理的综合应用,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
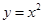 的焦点坐标是
的焦点坐标是  点时,拱顶离水面
点时,拱顶离水面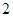 米,桥下的水面宽
米,桥下的水面宽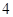 米;下午
米;下午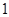 米,桥下的水面宽 米.
米,桥下的水面宽 米.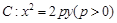 上一点
上一点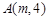 到其焦点的距离为
到其焦点的距离为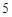 ,则m= .
,则m= .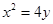 的准线方程为 .
的准线方程为 .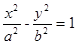 (a>0,b>0)上,C的焦距为4,则它的离心率为_____________.
(a>0,b>0)上,C的焦距为4,则它的离心率为_____________.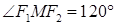 ,则双曲线离心率为
,则双曲线离心率为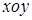 中,
中,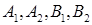 为椭圆
为椭圆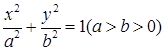 的
的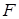 为其右焦点,直线
为其右焦点,直线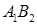 与直线
与直线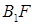 相交于点T,线段
相交于点T,线段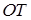 与椭圆的交点
与椭圆的交点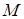 恰为线段
恰为线段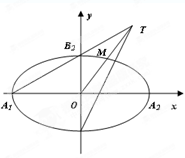
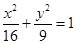 的左右焦点分别为
的左右焦点分别为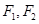 ,过焦点
,过焦点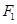 的直线交该椭圆于
的直线交该椭圆于 两点,若
两点,若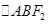 的内切圆面积为
的内切圆面积为 ,
, ,则
,则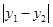 的值为 。
的值为 。