题目内容
16.已知P是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上的一点,F1,F2为椭圆的焦点.(1)若∠F1PF2=90°,求△PF1F2的面积;
(2)求|PF1|•|PF2|的最大值.
分析 (1)设|PF1|=m,|PF2|=n,由于∠F1PF2=90°,根据勾股定理与椭圆的定义可得:$\left\{\begin{array}{l}{m+n=10}\\{{m}^{2}+{n}^{2}=64}\end{array}\right.$,解出mn即可.
(2)设|PF1|=m,|PF2|=n,则m+n=10,利用基本不等式的性质即可得出.
解答 解:(1)c=$\sqrt{25-9}$=4,可得F1(-4,0),F2(4,0).
设|PF1|=m,|PF2|=n,
∵∠F1PF2=90°,
则$\left\{\begin{array}{l}{m+n=10}\\{{m}^{2}+{n}^{2}=64}\end{array}\right.$,化为mn=18.
∴△PF1F2的面积S=$\frac{1}{2}$mn=9.
(2)设|PF1|=m,|PF2|=n,
则m+n=10,
∴10$≥2\sqrt{mn}$,化为mn≤25,当且仅当m=n=5时取等号.
∴|PF1|•|PF2|的最大值为25.
点评 本题考查了椭圆的定义标准方程及其性质、勾股定理、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.函数f(x)=$\frac{1}{{\sqrt{2-{{log}_2}(1-x)}}}$的定义域为( )
| A. | (-3,+∞) | B. | $(-∞,\frac{1}{2})$ | C. | (-3,1) | D. | (0,1) |
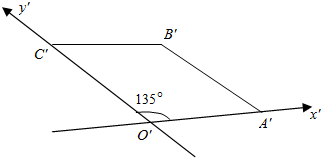 在直观图如图中,四边形O′A′B′C′为菱形且边长为2cm,则在xOy坐标系中原四边形OABC为矩形(填形状),面积为8cm2.
在直观图如图中,四边形O′A′B′C′为菱形且边长为2cm,则在xOy坐标系中原四边形OABC为矩形(填形状),面积为8cm2.