题目内容
18.已知数列{an}的通项公式an=4n-2n,其前n项和为Sn,则数列{$\frac{{2}^{n}}{{S}_{n}}$}的前n项和Tn=$\frac{3}{2}$•$\frac{{2}^{n+1}-2}{{2}^{n+1}-1}$.分析 通过分组法求和可知Sn=$\frac{4}{3}$(2n-1)(2n-$\frac{1}{2}$),进而裂项可知$\frac{{2}^{n}}{{S}_{n}}$=$\frac{3}{2}$•($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$),并项相加即得结论.
解答 解:∵an=4n-2n,
∴Sn=$\frac{4(1-{4}^{n})}{1-4}$-$\frac{2(1-{2}^{n})}{1-2}$=$\frac{1}{3}•$4n+1-2n+1+$\frac{2}{3}$=$\frac{4}{3}$(2n-1)(2n-$\frac{1}{2}$),
∴$\frac{{2}^{n}}{{S}_{n}}$=$\frac{{2}^{n}}{\frac{4}{3}({2}^{n}-1)({2}^{n}-\frac{1}{2})}$=$\frac{3}{2}$•$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{3}{2}$•($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$),
∴Tn=$\frac{3}{2}$•(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{7}$+…+$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$)
=$\frac{3}{2}$•(1-$\frac{1}{{2}^{n+1}-1}$)
=$\frac{3}{2}$•$\frac{{2}^{n+1}-2}{{2}^{n+1}-1}$,
故答案为:$\frac{3}{2}$•$\frac{{2}^{n+1}-2}{{2}^{n+1}-1}$.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | {x|0<x<1} | B. | {x|x<1} | C. | {x|0<x≤1} | D. | {x|x≤1} |
| A. | 若f(x1)=f(x2),则x1-x2=kπ,k∈Z | |
| B. | f(x)的图象关于点($-\frac{3}{8}π$,0)对称 | |
| C. | f(x)的图象关于直线$x=\frac{5}{8}π$对称 | |
| D. | f(x)的图象向右平移$\frac{π}{4}$个单位长度后得$g(x)=\sqrt{2}sin(2x+\frac{π}{4})$ |
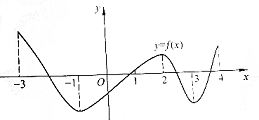 已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.
已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.