题目内容
(08年长宁区质量抽测理) 已知![]() 的周长为
的周长为![]() ,且
,且![]() 。
。
(1)求边![]() 的长;(2)若
的长;(2)若![]() 的面积为
的面积为![]() ,求角
,求角![]() 的度数。
的度数。
解析:(1)由正弦定理得![]() ,
,
![]() ,
,![]() ,因此
,因此![]() 。
。
(2)![]() 的面积
的面积![]() ,
,![]() ,
,
又![]() ,
,
所以由余弦定理得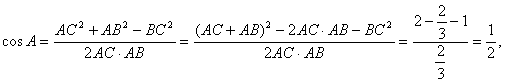

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
(08年长宁区质量抽测理) 已知![]() 的周长为
的周长为![]() ,且
,且![]() 。
。
(1)求边![]() 的长;(2)若
的长;(2)若![]() 的面积为
的面积为![]() ,求角
,求角![]() 的度数。
的度数。
解析:(1)由正弦定理得![]() ,
,
![]() ,
,![]() ,因此
,因此![]() 。
。
(2)![]() 的面积
的面积![]() ,
,![]() ,
,
又![]() ,
,
所以由余弦定理得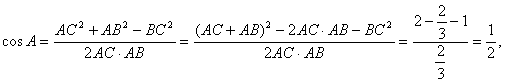

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案