题目内容
如图:已知四棱锥P-ABCD,底面是边长为3的正方形ABCD,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.(1)求证:AB⊥MN;
(2)若MN=5,求二面角N-AM-B的余弦值.

【答案】分析:(1)四棱锥P-ABCD的底面是边长为3的正方形ABCD,且PA⊥面ABCD,由此得到AD,AB,AP两两互相垂直,分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系,设出AP长度,则可得到图中各点坐标,求出向量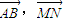 ,由它们的数量积等于0证得AB⊥MN;
,由它们的数量积等于0证得AB⊥MN;
(2)利用MN=5,求出AP的长度,分别求出平面AMB和平面AMN的一个法向量,利用两个平面的法向量所成的角求二面角N-AM-B的余弦值.
解答: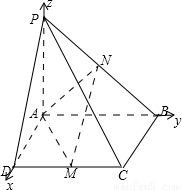 (1)证明:因为底面是边长为3的正方形,PA⊥面ABCD,
(1)证明:因为底面是边长为3的正方形,PA⊥面ABCD,
所以AP⊥AD⊥AB.如图,
分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系,设PA=t
则
得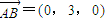 ,
,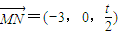 .
.
∴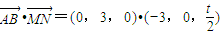 =0,所以AB⊥MN;
=0,所以AB⊥MN;
(2)解:由 ,得
,得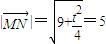 ,
,
解得t=8,即PA=8.
取平面AMB的一个法向量为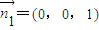
设平面AMN的法向量 ,又
,又 ,
,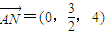
由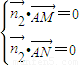 得:
得: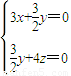 ,取y=-2,得x=1,z=
,取y=-2,得x=1,z= .
.
所以平面AMN的一个法向量是 ,
,
设二面角N-AM-B为α,则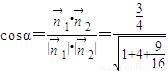 =
=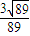 .
.
所以二面角N-AM-B的余弦值为 .
.
点评:本题考查了直线与平面垂直的性质,考查了利用空间向量求二面角的大小,利用空间向量求二面角的大小时,关键是分清两个平面的法向量所成的角与二面角的关系,此题是中档题.
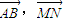 ,由它们的数量积等于0证得AB⊥MN;
,由它们的数量积等于0证得AB⊥MN;(2)利用MN=5,求出AP的长度,分别求出平面AMB和平面AMN的一个法向量,利用两个平面的法向量所成的角求二面角N-AM-B的余弦值.
解答:
 (1)证明:因为底面是边长为3的正方形,PA⊥面ABCD,
(1)证明:因为底面是边长为3的正方形,PA⊥面ABCD,所以AP⊥AD⊥AB.如图,
分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系,设PA=t
则

得
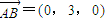 ,
,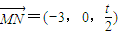 .
.∴
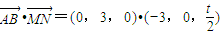 =0,所以AB⊥MN;
=0,所以AB⊥MN;(2)解:由
 ,得
,得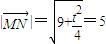 ,
,解得t=8,即PA=8.
取平面AMB的一个法向量为
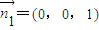
设平面AMN的法向量
 ,又
,又 ,
,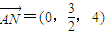
由
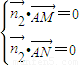 得:
得: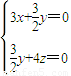 ,取y=-2,得x=1,z=
,取y=-2,得x=1,z= .
.所以平面AMN的一个法向量是
 ,
,设二面角N-AM-B为α,则
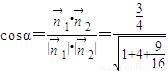 =
=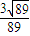 .
.所以二面角N-AM-B的余弦值为
 .
.点评:本题考查了直线与平面垂直的性质,考查了利用空间向量求二面角的大小,利用空间向量求二面角的大小时,关键是分清两个平面的法向量所成的角与二面角的关系,此题是中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,