Question

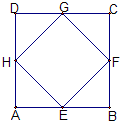（2010•台州二模）如图，E，F，G，H分别是正方形ABCD各边的中点，将等腰    三角形EFB，FGC，GHD，HEA分别沿其底边折起，使其与原 所在平面成直二面角，则所形成的空间图形中，共有异面直线 段的对数为

28

．

Answer 1

分析：先画出将等腰三角形EFB，FGC，GHD，HEA分别沿其底边折起，使其与原 所在平面成直二面角，则所形成的空间图形如图所示，结合图形分析在所形成的空间图形中，异面直线分成两类：一类是：平面EFGH外的直线，如AH与CF，DG，BE这样的；另一类是：平面EFGH外的直线与平面EFGH内的直线，如AH与GF，EF这样的，最后利用加法原理求得所形成的空间图形中，共有异面直线的对数即可．

解答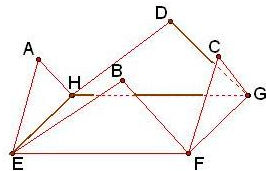：解：将等腰三角形EFB，FGC，GHD，HEA分别沿其底边折起，使其与原 所在平面成直二面角，则所形成的空间图形如图所示，
则所形成的空间图形中，异面直线分成两类：
一类是：平面EFGH外的直线，如AH与CF，DG，BE这样的共有：8×3÷2=12对；
另一类是：平面EFGH外的直线与平面EFGH内的直线，如AH与GF，EF这样的共有：8×2=16．
则所形成的空间图形中，共有异面直线的对数为：12+16=28对．
故答案为：28．

点评：本小题主要考查异面直线的判定、异面直线等基础知识，考查空间想象能力，考查分类讨论思想．属于中档题．