题目内容
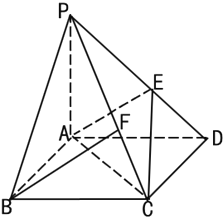
【题目】如图,底面是平行四边形的四棱锥![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 平面
平面![]() ,则
,则![]() ______.
______.
【答案】![]()
【解析】
取棱PC上的点F,使![]()
![]() ,取棱PD上的点M使
,取棱PD上的点M使![]()
![]() ,连接BD.设BD∩AC=O.结合平行四边形的性质及三角形中位线定理及面面平行的判定定理可得平面BMF∥平面AEC,进而由面面平行的性质得到BF∥平面AEC.
,连接BD.设BD∩AC=O.结合平行四边形的性质及三角形中位线定理及面面平行的判定定理可得平面BMF∥平面AEC,进而由面面平行的性质得到BF∥平面AEC.
存在点F满足![]()
![]() 使BF∥平面AEC
使BF∥平面AEC
理由如下:
取棱PC上的点F,使![]()
![]() ,取棱PD上的点M使
,取棱PD上的点M使![]()
![]() ,则E为MD中点,
,则E为MD中点,
连接BD.设BD∩AC=O.
连接BM,OE.
∵![]()
![]() =
=![]() ,F为PC的中点,E是MD的中点,
,F为PC的中点,E是MD的中点,
∴MF∥EC,BM∥OE.
∵MF平面AEC,CE平面AEC,BM平面AEC,OE平面AEC,
∴MF∥平面AEC,BM∥平面AEC.
∵MF∩BM=M,
∴平面BMF∥平面AEC.
又BF平面BMF,
∴BF∥平面AEC.
故答案为:![]()

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在(195,210]内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图
图1:乙流水线样本频率分布直方图
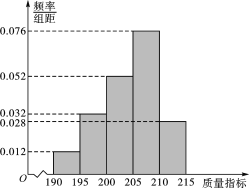
表1:甲流水线样本频数分布表
质量指标值 | 频数 |
(190,195] | 9 |
(195,200] | 10 |
(200,205] | 17 |
(205,210] | 8 |
(210,215] | 6 |
(1)根据图1,估计乙流水线生产产品该质量指标值的中位数和平均数(估算平均数时,同一组中的数据用该组区间的中点值为代表);
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出的不合格品约多少件?