题目内容
(推理)三角形的内角和为180º,凸四边形内角和为360º,那么凸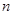 边形的内角和为
边形的内角和为
A.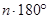 | B.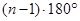 | C.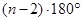 | D.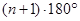 |
C
解析试题分析:由三角形的内角和为180º,凸四边形内角和为360º,可推理得到,边数与180°的关系,即边数减2与180°的乘积,所以,凸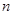 边形的内角和为
边形的内角和为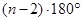 ,选C。
,选C。
考点:归纳推理
点评:简单题,归纳推理是由部分到整体的推理。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
| A.假设三内角都大于60度; |
| B.假设三内角都不大于60度; |
| C.假设三内角至多有一个大于60度; |
| D.假设三内角至多有两个大于60度。 |
在应用数学归纳法证明凸n变形的对角线为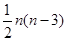 条时,第一步检验n等于( )
条时,第一步检验n等于( )
| A.1 | B.2 | C.3 | D.0 |
下列推理合理的是( )
A.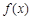 是增函数,则 是增函数,则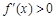 |
B.因为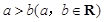 ,则 ,则 |
C.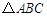 为锐角三角形,则 为锐角三角形,则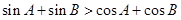 |
D.直线 ,则 ,则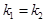 |
对命题“正三角形的内切圆切于三边的中点”可类比猜想出:正四面体的内切球切于四面都为正三角形的什么位置?( )
| A.正三角形的顶点 | B.正三角形的中心 |
| C.正三角形各边的中点 | D.无法确定 |
如下图,根据图中的数构成的规律,a所表示的数是( ) 
| A.12 | B.48 | C.60 | D.144 |
用数学归纳法证明: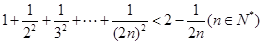 ,第二步证明“从
,第二步证明“从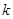 到
到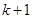 ”,左端增加的项数是( )
”,左端增加的项数是( )
A.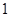 | B.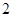 | C.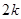 | D.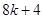 |
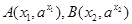 是函数
是函数 的图象上任意不同两点,依据图象可知,线段AB总是位于A、B两点之间函数图象的上方,因此有结论
的图象上任意不同两点,依据图象可知,线段AB总是位于A、B两点之间函数图象的上方,因此有结论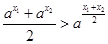 成立.运用类比思想方法可知,若点
成立.运用类比思想方法可知,若点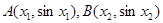 是函数
是函数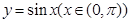 的图象上任意不同两点,则类似地有_________________成立.
的图象上任意不同两点,则类似地有_________________成立.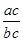 =
=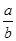 ”类比得到“
”类比得到“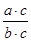 =
=