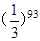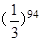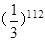题目内容
观察下列等式,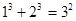 ,
,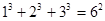 ,
,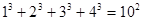 根据上述规律,
根据上述规律,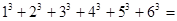 ( )
( )
A.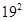 | B.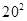 | C.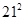 | D.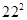 |
C
解析试题分析: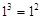 .下面考查1,3,6,10的规律,由于
.下面考查1,3,6,10的规律,由于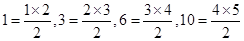 ,由此可猜想,
,由此可猜想,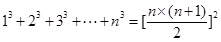 ,所以
,所以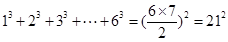 .
.
考点:归纳推理.

练习册系列答案
相关题目
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
| A.假设三内角都大于60度; |
| B.假设三内角都不大于60度; |
| C.假设三内角至多有一个大于60度; |
| D.假设三内角至多有两个大于60度。 |
对命题“正三角形的内切圆切于三边的中点”可类比猜想出:正四面体的内切球切于四面都为正三角形的什么位置?( )
| A.正三角形的顶点 | B.正三角形的中心 |
| C.正三角形各边的中点 | D.无法确定 |
在数列{an}中,an=1- +
+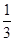 -
-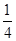 +…+
+…+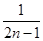 -
-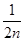 ,则ak+1等于( )
,则ak+1等于( )
A.ak+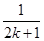 | B.ak+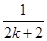 - -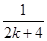 |
C.ak+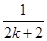 | D.ak+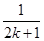 - -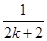 |
有两种花色的正六边形地面砖,按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是( ).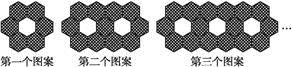
| A.26 | B.31 | C.32 | D.36 |
学习合情推理后,甲、乙两位同学各举了一个例子,
甲:由“若三角形周长为l,面积为S,则其内切圆半径r=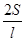 ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r=
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r=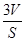 ”;
”;
乙:由“若直角三角形两直角边长分别为a、b,则其外接圆半径r=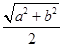 ”类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径r=
”类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径r=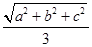 ”.这两位同学类比得出的结论( )
”.这两位同学类比得出的结论( )
| A.两人都对 | B.甲错、乙对 |
| C.甲对、乙错 | D.两人都错 |
已知n是正偶数,用数学归纳法证明时,若已假设n=k(k≥2且为偶数)时命题为真,则还需证明( )
| A.n=k+1时命题成立 |
| B.n=k+2时命题成立 |
| C.n=2k+2时命题成立 |
| D.n=2(k+2)时命题成立 |
 、
、 、
、 、
、 、
、 按表
按表 的方式进行排列,记
的方式进行排列,记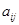 表示第
表示第 行和第
行和第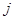 列的数,若
列的数,若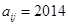 ,则
,则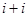 的值为( )
的值为( )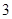 列
列 列
列
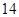


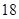
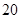
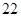
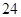


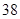
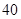
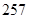 B.
B.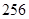 C.
C.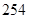 D.
D.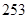
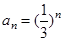 ,把数列
,把数列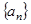 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,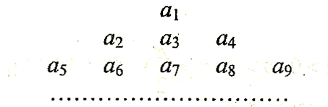
 表示第
表示第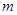 行的第
行的第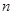 个数,则
个数,则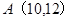 = ( )
= ( )