题目内容
1.已知椭圆C的离心率为$\frac{2}{3}$,且与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$有相同的焦点,则椭圆C的标准方程为$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{20}=1$.分析 由$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$求出a,b,以及焦点所在的坐标轴,由a、b、c的关系求出c,即可得到焦点坐标,再由题意和离心率公式求出椭圆C的标准方程.
解答 解:由$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$得,a=5、b=3,且焦点在x轴上,
则c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{25-9}$=4,
∴椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$的焦点的坐标为(-4,0)、(4,0),
∵椭圆C的离心率为$\frac{2}{3}$,且c=4,∴$\frac{c}{a}$=$\frac{2}{3}$,a=6,
则b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{36-16}$=$\sqrt{20}$,
∴椭圆C的标准方程是$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{20}=1$,
故答案为:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{20}=1$.
点评 本题考查椭圆的方程和性质,掌握椭圆的a,b,c的关系和焦点的位置是解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
11.若x,y满足约束条件$\left\{\begin{array}{l}x+y≥1\\ x-y≥-1\\ 2x-y≤2\end{array}\right.$,目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )
| A. | (-1,2 ) | B. | (-4,2 ) | C. | (-4,0] | D. | (-2,4) |
12.如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( )
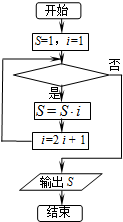

| A. | i≤31? | B. | i≤63? | C. | i≥63? | D. | i≤127? |
10.若sin2xsin3x=cos2xcos3x,则x的值是( )
| A. | $\frac{π}{10}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{5}$ | D. | $\frac{π}{4}$ |
 有下列四个结论,
有下列四个结论,
