题目内容
(本小题满分12分)
设二次函数f(x)=ax2+bx(a≠0)满足条件:
①f(-1+x)=f(-1-x);②函数f(x)的图象与直线y=x只有一个公共点.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若不等式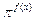 >(
>(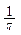 )2-tx在t∈[-2,2]时恒成立,求实数x的取值范围.
)2-tx在t∈[-2,2]时恒成立,求实数x的取值范围.
设二次函数f(x)=ax2+bx(a≠0)满足条件:
①f(-1+x)=f(-1-x);②函数f(x)的图象与直线y=x只有一个公共点.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若不等式
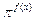 >(
>(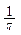 )2-tx在t∈[-2,2]时恒成立,求实数x的取值范围.
)2-tx在t∈[-2,2]时恒成立,求实数x的取值范围.(Ⅰ)函数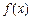 的解析式为
的解析式为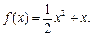
(Ⅱ)实数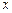 的取值范围是
的取值范围是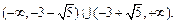
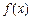 的解析式为
的解析式为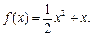
(Ⅱ)实数
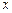 的取值范围是
的取值范围是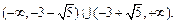
解:(Ⅰ)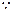 由①知
由①知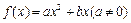 的对称轴方程是
的对称轴方程是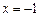 ,
,
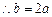 ;……………………………………………………………………………1分
;……………………………………………………………………………1分
 函数
函数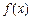 的图象与直线
的图象与直线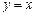 只有一个公共点,
只有一个公共点,
 方程组
方程组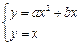 有且只有一解,即
有且只有一解,即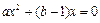 有两个相同的实根;
有两个相同的实根;
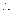 Δ=
Δ=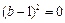 ,即
,即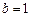 ,
,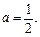 ………………………………………3分
………………………………………3分
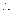 函数
函数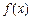 的解析式为
的解析式为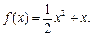 …………………………………………4分
…………………………………………4分
(Ⅱ)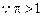 ,
,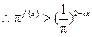 等价于
等价于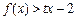 ,…………………………6分
,…………………………6分
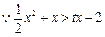 在
在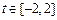 时恒成立等价于
时恒成立等价于
函数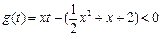 在
在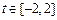 时恒成立;……………………9分
时恒成立;……………………9分
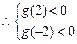 ,即
,即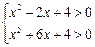 ,
,
解得: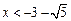 或
或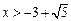 ,
,
综上:实数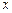 的取值范围是
的取值范围是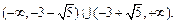 ………………………12分
………………………12分
 由①知
由①知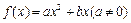 的对称轴方程是
的对称轴方程是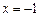 ,
,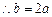 ;……………………………………………………………………………1分
;……………………………………………………………………………1分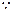 函数
函数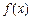 的图象与直线
的图象与直线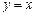 只有一个公共点,
只有一个公共点,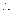 方程组
方程组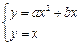 有且只有一解,即
有且只有一解,即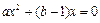 有两个相同的实根;
有两个相同的实根;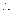 Δ=
Δ=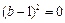 ,即
,即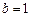 ,
,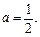 ………………………………………3分
………………………………………3分 函数
函数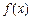 的解析式为
的解析式为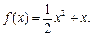 …………………………………………4分
…………………………………………4分(Ⅱ)
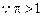 ,
,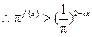 等价于
等价于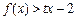 ,…………………………6分
,…………………………6分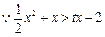 在
在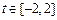 时恒成立等价于
时恒成立等价于函数
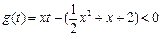 在
在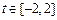 时恒成立;……………………9分
时恒成立;……………………9分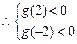 ,即
,即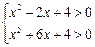 ,
,解得:
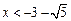 或
或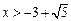 ,
,综上:实数
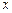 的取值范围是
的取值范围是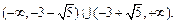 ………………………12分
………………………12分
练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
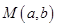 在函数
在函数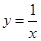 的图象上,点N与点M关于
的图象上,点N与点M关于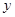 轴对称且在直线
轴对称且在直线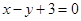 上,则函数
上,则函数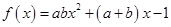 在区间
在区间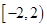 上 ( )
上 ( ) ,无最大值
,无最大值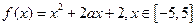 .
.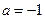 时,求函数的最大值和最小值
时,求函数的最大值和最小值 ;
;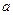 的取值范围,使
的取值范围,使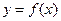 在区间
在区间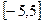 上是单调函数,并指出相应的单调性.
上是单调函数,并指出相应的单调性. 的解集为
的解集为 ,则函数
,则函数 的图象为( )
的图象为( )
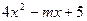 的对称轴为
的对称轴为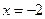 ,则f(1)的值为 ( )
,则f(1)的值为 ( )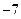
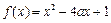 在区
在区 间 [-2,4] 上是单调函数的条件是( )
间 [-2,4] 上是单调函数的条件是( )


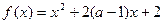 在区间
在区间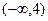 上是减函数,则实数
上是减函数,则实数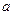 的取值范围是____________.
的取值范围是____________.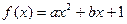 是定义在
是定义在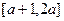 上的偶函数,那么
上的偶函数,那么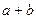 的值为( )
的值为( )



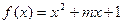 的图像关于直线
的图像关于直线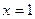 对称的充要条件是 ( )
对称的充要条件是 ( )


