题目内容
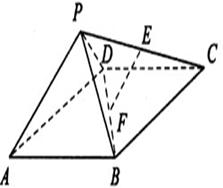
四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)求证:EF∥面PAD;
(2)求证:面PDC⊥面PAB;
(1)求证:EF∥面PAD;
(2)求证:面PDC⊥面PAB;

(1)如图,连接AC,∵ABCD为矩形,且F是BD的中点,∴AC必经过F ……………….2分
又E是PC的中点,
所以,EF∥AP. ……………4分
∵EF在面PAD外,PA在面内
∴EF∥面PAD……………6分
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD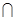 面ABCD=AD,∴CD⊥面PAD,
面ABCD=AD,∴CD⊥面PAD,
又AP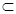 面PAD,∴AP⊥CD. ……………………8分
面PAD,∴AP⊥CD. ……………………8分
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD.……………10分
又AP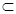 面PAB,所以,面PAB⊥面PDC. ……………………12分
面PAB,所以,面PAB⊥面PDC. ……………………12分
又E是PC的中点,
所以,EF∥AP. ……………4分
∵EF在面PAD外,PA在面内
∴EF∥面PAD……………6分
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD
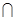 面ABCD=AD,∴CD⊥面PAD,
面ABCD=AD,∴CD⊥面PAD,又AP
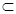 面PAD,∴AP⊥CD. ……………………8分
面PAD,∴AP⊥CD. ……………………8分又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD.……………10分
又AP
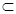 面PAB,所以,面PAB⊥面PDC. ……………………12分
面PAB,所以,面PAB⊥面PDC. ……………………12分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
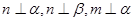
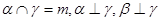
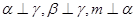
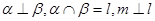
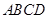 中,
中,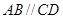 ,
,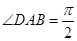 ,点
,点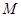 、
、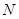 分别在
分别在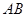 ,
,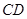 上,且
上,且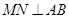 ,
,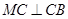 ,
, ,
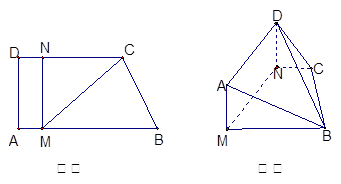
,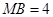 ,现将梯形
,现将梯形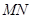 折起,使平面
折起,使平面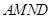 与平面
与平面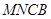 垂直(如图乙).
垂直(如图乙).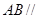 平面
平面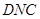 ;
;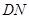 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为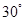 ?
?
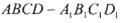 棱长为1,点
棱长为1,点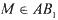 ,
,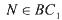 ,且
,且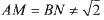 ,有以下四个结论:
,有以下四个结论: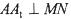 ,②
,②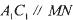 ;③.
;③.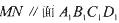 ;④MN与
;④MN与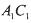 是异面直线、其中正确结论的序号是________ (注:把你认为正确命题的序号都填上)
是异面直线、其中正确结论的序号是________ (注:把你认为正确命题的序号都填上)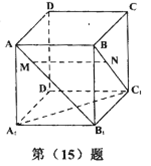
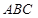 为底面的直棱柱
为底面的直棱柱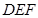 所截而得.
所截而得. 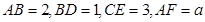 ,
,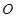 为
为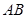 的中点.
的中点.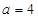 时,求平面
时,求平面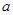 为何值时,在棱
为何值时,在棱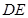 上存在点
上存在点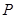 ,使
,使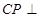 平面
平面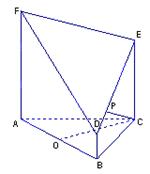
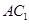 中,点
中,点 分别在棱
分别在棱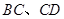 上,满足
上,满足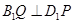 ,
,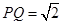 .
.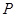 、
、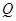 两点的位置.
两点的位置.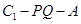 大小的余弦值.
大小的余弦值.
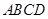 中,
中,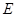 是
是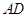 中点,
中点,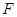 是
是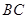 中点,
中点,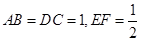 ,则直
,则直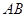 与
与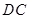 所成的角大小为( )
所成的角大小为( )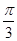
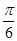
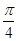
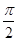
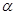 、
、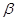 是两个不同的平面,给出下列四个命题.
是两个不同的平面,给出下列四个命题.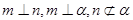 ,则
,则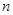 ∥
∥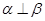 ,
,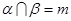 ,
,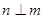 ,则
,则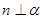 或
或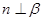 ;
;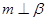 ,
,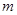 ∥
∥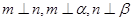 ,则
,则