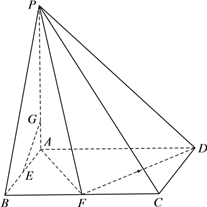
[题目]如图.四棱锥P-ABCD中.底面ABCD是矩形.PA面ABCD.且AB＝2.AD＝4.AP＝4.F是线段BC的中点.⑴ 求证:面PAF面PDF,⑵ 若E是线段AB的中点.在线段AP上是否存在一点G.使得EG面PDF?若存在.求出线段AG的长度,若不存在.说明理由. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，四棱锥P-ABCD中，底面ABCD是矩形，PA面ABCD，且AB＝2，AD＝4，

AP＝4，F是线段BC的中点.

⑴ 求证：面PAF面PDF；

⑵ 若E是线段AB的中点，在线段AP上是否存在一点G，使得EG面PDF？若存在，求出线段AG的长度；若不存在，说明理由.

【答案】(1)详见解析;(2)详见解析.

【解析】试题分析：（1）PA面ABCD，面ABCD， PADF ，在矩形内根据F是线段BC的中点和长度，根据勾股定理求得AFDF，即得证 (2)解法一：延长AB交DF延长线于点M，连结PM.这样将面PDF延伸，当EGPM时存在一点G，使得EG面PDF 解法二：构造平行四边形，取DF中点I，连结EI，过点G作AD的平行线交PD于点H，连结GH、HI.证得四边形GEIH是平行四边形，根据线面平行判定定理即可证得。

解析：⑴ PA面ABCD，面ABCD， PADF，

又在底面ABCD中，，，

， AFDF，

， DF面PAF，

面PDF，面PAF面PDF.

解⑵：法一、假设在线段AP上存在点G，使得EG面PDF.连结AB并延长交DF延长线于点M，连结PM.

F是线段BC的中点，底面ABCD是矩形，

，

EG面PDM，面PAM，面PAM 面PDM=PM，

EGPM，

，，

故在线段AP上存在点G，使得EG面PDF，此时.

法二、假设在线段AP上存在点G，使得EG面PDF.取DF中点I，连结EI，过点G作AD的平行线交PD于点H，连结GH、HI.

E是线段AB的中点，是梯形ABFD的中位线，

，EIGH，

EG面PDF，面GEIH，面GEIH 面PDM=IH，

EGIH，

四边形GEIH是平行四边形，

，

，，

故在线段AP上存在点G，使得EG面PDF，此时.

练习册系列答案

【题目】已知函数f（x）＝．

（l）求函数f（x）的定义域；

（2）求函数f（x）的值域．

【题目】已知函数， .

（Ⅰ）若曲线在点处的切线与直线垂直，求函数的极值；

（Ⅱ）设函数.当时，若区间上存在，使得，求实数的取值范围.（为自然对数底数）

【题目】某个体户计划经销A、B两种商品，据调查统计，当投资额为x（x≥0）万元时，在经销A、B商品中所获得的收益分别为f（x）万元与g（x）万元、其中f（x）=a（x﹣1）+2（a＞0）；g（x）=6ln（x+b），（b＞0）已知投资额为零时，收益为零．
（1）试求出a、b的值；
（2）如果该个体户准备投入5万元经营这两种商品，请你帮他制定一个资金投入方案，使他能获得最大收益，并求出其收入的最大值．（精确到0.1，参考数据：ln3≈1.10）．

【题目】由小到大排列的一组数据x1 ， x2 ， x3 ， x4 ， x5 ，其中每个数据都小于﹣1，则样本1，x1 ， ﹣x2 ， x3 ， ﹣x4 ， x5的中位数为（）
A.
B.
C.
D.

【题目】设a≥0，f（x）=x﹣1﹣ln2x+2alnx（x＞0）．
（1）令F（x）=xf′（x），讨论F（x）在（0，+∞）内的单调性并求极值；
（2）求证：当x＞1时，恒有x＞ln2x﹣2alnx+1．

【题目】如图，在三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AB=AC，D，D1分别是线段BC，B1C1的中点，P是线段AD上异于端点的点．
（1）在平面ABC内，试作出过点P与平面A1BC平行的直线l，并说明理由；
（2）证明：直线l⊥平面ADD1A1 ．

【题目】已知函数f（x）=lnx﹣a2x2+ax（a∈R）．
（1）当a=1时，求函数f（x）最大值；
（2）若函数f（x）在区间（1，+∞）上是减函数，求实数a的取值范围．

试题分类