Question

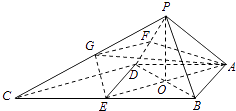
【题目】如图，四棱锥P﹣ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是等边三角形．

（1）证明：PB⊥CD；
（2）求二面角A﹣PD﹣C的大小．

Answer 1

【答案】
（1）证明：取BC的中点E，连接DE，可得四边形ABED是正方形

过点P作PO⊥平面ABCD，垂足为O，连接OA、OB、OD、OE

∵△PAB与△PAD都是等边三角形，∴PA=PB=PD，可得OA=OB=OD

因此，O是正方形ABED的对角线的交点，可得OE⊥OB

∵PO⊥平面ABCD，得直线OB是直线PB在内的射影，∴OE⊥PB

∵△BCD中，E、O分别为BC、BD的中点，∴OE∥CD，可得PB⊥CD；

（2）解：由（1）知CD⊥PO，CD⊥PB

∵PO、PB是平面PBD内的相交直线，∴CD⊥平面PBD

∵PD平面PBD，∴CD⊥PD

取PD的中点F，PC的中点G，连接FG，

则FG为△PCD有中位线，∴FG∥CD，可得FG⊥PD

连接AF，由△PAD是等边三角形可得AF⊥PD，∴∠AFG为二面角A﹣PD﹣C的平面角

连接AG、EG，则EG∥PB

∵PB⊥OE，∴EG⊥OE，

设AB=2，则AE=2 ，EG= PB=1，故AG= =3

在△AFG中，FG= CD= ，AF= ，AG=3

∴cos∠AFG= =﹣ ，得∠AFG=π﹣arccos ，

即二面角A﹣PD﹣C的平面角大小是π﹣arccos ．

【解析】（1）取BC的中点E，连接DE，过点P作PO⊥平面ABCD于O，连接OA、OB、OD、OE．可证出四边形ABED是正方形，且O为正方形ABED的中心．因此OE⊥OB，结合三垂线定理，证出OE⊥PB，而OE是△BCD的中位线，可得OE∥CD，因此PB⊥CD；（2）由（1）的结论，证出CD⊥平面PBD，从而得到CD⊥PD．取PD的中点F，PC的中点G，连接FG，可得FG∥CD，所以FG⊥PD．连接AF，可得AF⊥PD，因此∠AFG为二面角A﹣PD﹣C的平面角，连接AG、EG，则EG∥PB，可得EG⊥OE．设AB=2，可求出AE、EG、AG、AF和FG的长，最后在△AFG中利用余弦定理，算出∠AFG=π﹣arccos ，即得二面角A﹣PD﹣C的平面角大小．
【考点精析】本题主要考查了直线与平面垂直的性质和共线向量与共面向量的相关知识点，需要掌握垂直于同一个平面的两条直线平行；向量共线的充要条件：对于空间任意两个向量，，的充要条件是存在实数，使才能正确解答此题．