题目内容
9.平面上有两条相距2a的平行线,把一枚半径为r(r<a)的硬币任意掷在两线之间,则硬币不与任何一条直线相碰的概率是$\frac{a-r}{a}$.分析 为了确定硬币的位置,由硬币中心O向靠得最近的平行线引垂线OM,垂足为M,这样线段OM长度|OM|的取值范围就是[0,a],只有当r<|OM|≤a时,硬币不与平行线相碰,最后根据几何概型的概率公式解之即可.
解答 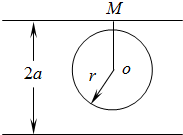 解:把“硬币不与任一条平行线相碰”的事件记为事件A,
解:把“硬币不与任一条平行线相碰”的事件记为事件A,
为了确定硬币的位置,由硬币中心O向靠得最近的平行线引垂线OM,垂足为M,
如图所示,这样线段OM长度|OM|的取值范围就是[0,a],
只有当r<|OM|≤a时,硬币不与平行线相碰,
所以所求事件A的概率就是$\frac{a-r}{a}$.
故答案为:$\frac{a-r}{a}$.
点评 本题主要考查了几何概型,解题的关键确定硬币的位置,同时考查了分析问题的能力,属于中档题

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
20.下列函数中,既是奇函数又在其定义域上是增函数的是( )
| A. | y=-$\frac{2}{x}$ | B. | y=2x | C. | y=log2x | D. | y=2x |
1.已知实数a=log${\;}_{\frac{1}{3}}$2,b=log2e,c=($\frac{1}{3}$)0.4,则a,b,c的大小顺序为( )
| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | b<c<a |
18.一种团体竞技比赛的积分规则是:每队胜、平、负分别得2分、1分、0分,已知甲球队已赛4场,积4分,在这4场比赛中,甲球队胜、平、负(包括顺序)的情况共有( )
| A. | 7种 | B. | 13种 | C. | 18种 | D. | 19种 |
19.在正项等比数列{an}中,若a1=1,且3a3,a2,2a4成等差数列,则log2(a1•a2•a3•a4•a5•a6•a7)=( )
| A. | -28 | B. | -21 | C. | 21 | D. | 28 |