题目内容
已知函数
(I)若直线l1交函数f(x)的图象于P,Q两点,与l1平行的直线 与函数
与函数 的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
(II)若不等式 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(III)求证: 〔其中
〔其中 , e为自然对数的底数)
, e为自然对数的底数)

(I)若直线l1交函数f(x)的图象于P,Q两点,与l1平行的直线
 与函数
与函数 的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
的图象切于点R,求证 P,R,Q三点的横坐标成等差数列; (II)若不等式
 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(III)求证:
 〔其中
〔其中 , e为自然对数的底数)
, e为自然对数的底数)(Ⅰ)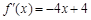 ,设切点R(x0,y0)
,设切点R(x0,y0)
则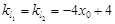 .
.
令l2:y=(-4x0+4)x+b.
联立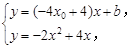 消去y得 2x2-4x0x+b=0.
消去y得 2x2-4x0x+b=0.
令P(x1,y1),Q(x2,y2),则x1+x2=2x0,
即R、R、Q三点的横坐标成等差数列. ……………………………………4分
(Ⅱ)由已知有f (x)+g(x)-4x=-2x2+alnx≤0恒成立,
令F(x)=2x2-alnx(x>0),
则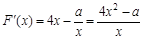 .
.
由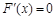 ,得
,得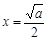 .
.
当0<x<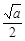 时
时 ,F(x)在区
,F(x)在区 间(0,
间(0,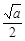 )上递减;
)上递减;
当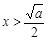 时,
时,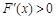 ,F(x)在区间(
,F(x)在区间(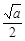 ,+∞)上递增.
,+∞)上递增.
∴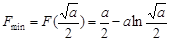 ≥0,得0<a≤4e.……………………………9分
≥0,得0<a≤4e.……………………………9分
(Ⅲ)由(2)知当a=2e时有2x2-2elnx≥0,得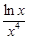 ≤
≤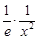
∴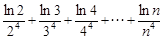
≤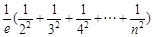
<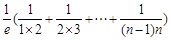
=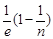
<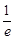 .
.
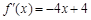 ,设切点R(x0,y0)
,设切点R(x0,y0)则
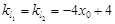 .
.令l2:y=(-4x0+4)x+b.
联立
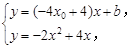 消去y得 2x2-4x0x+b=0.
消去y得 2x2-4x0x+b=0.令P(x1,y1),Q(x2,y2),则x1+x2=2x0,
即R、R、Q三点的横坐标成等差数列. ……………………………………4分
(Ⅱ)由已知有f (x)+g(x)-4x=-2x2+alnx≤0恒成立,
令F(x)=2x2-alnx(x>0),
则
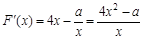 .
.由
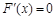 ,得
,得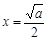 .
.当0<x<
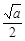 时
时 ,F(x)在区
,F(x)在区 间(0,
间(0,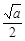 )上递减;
)上递减;当
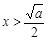 时,
时,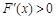 ,F(x)在区间(
,F(x)在区间(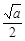 ,+∞)上递增.
,+∞)上递增.∴
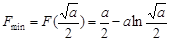 ≥0,得0<a≤4e.……………………………9分
≥0,得0<a≤4e.……………………………9分(Ⅲ)由(2)知当a=2e时有2x2-2elnx≥0,得
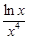 ≤
≤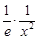
∴
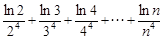
≤
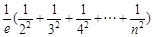
<
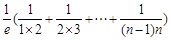
=
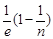
<
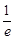 .
.略

练习册系列答案
相关题目
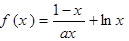
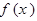 在
在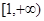 上为增函数,求正实数
上为增函数,求正实数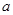 的取值范围;
的取值范围;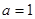 时,求函数
时,求函数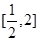 上的最值;
上的最值;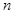 ,试比较
,试比较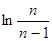 与
与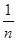 的大小关系.
的大小关系. 的图象是连续不断的,且
的图象是连续不断的,且 ,
, ,则下列命题正确的是( ).
,则下列命题正确的是( ). ,
, 是二次函数,当
是二次函数,当 时,
时, ,且
,且 为奇函数,求函数
为奇函数,求函数
 有两个解,则
有两个解,则 的取值范围是( )
的取值范围是( )



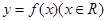 满足
满足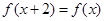 且
且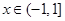 时
时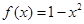 ,函数
,函数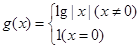 ,则函数
,则函数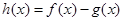 在区间
在区间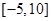 内零点的个数为( )
内零点的个数为( )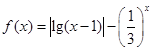 有两个零点x1,x2,则有
有两个零点x1,x2,则有



 的实数根x0叫做函数
的实数根x0叫做函数 的“新驻点”,如
的“新驻点”,如 果函数
果函数 ,
, ,
, (
( )的“新驻点”分别为
)的“新驻点”分别为 ,
, ,
, ,那么
,那么 如果
如果 ,则实数
,则实数 ▲
▲