题目内容
已知函数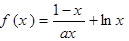
(1)若函数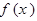 在
在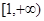 上为增函数,求正实数
上为增函数,求正实数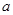 的取值范围;
的取值范围;
(2)当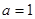 时,求函数
时,求函数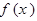 在
在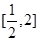 上的最值;
上的最值;
(3)当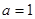 时,对大于1的任意正整数
时,对大于1的任意正整数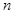 ,试比较
,试比较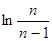 与
与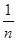 的大小关系.
的大小关系.
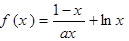
(1)若函数
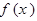 在
在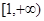 上为增函数,求正实数
上为增函数,求正实数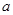 的取值范围;
的取值范围;(2)当
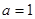 时,求函数
时,求函数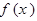 在
在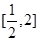 上的最值;
上的最值;(3)当
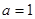 时,对大于1的任意正整数
时,对大于1的任意正整数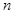 ,试比较
,试比较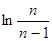 与
与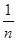 的大小关系.
的大小关系.1)因为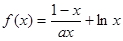 ,所以
,所以
因为函数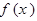 在
在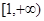 上为增函数,所以
上为增函数,所以 对
对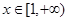 恒成立,
恒成立,
所以 对
对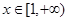 恒成立,即
恒成立,即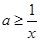 对
对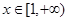 恒成立,所以
恒成立,所以 .……4分
.……4分
(2)当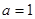 时,
时,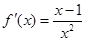 ,所以当
,所以当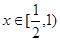 时,
时, ,故
,故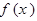 在
在 上单调递减;当
上单调递减;当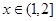 ,
,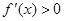 ,故
,故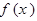 在
在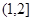 上单调递增,所以
上单调递增,所以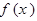 在区间
在区间 上有唯一极小值点,故
上有唯一极小值点,故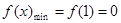 ,又
,又 ,
, ,
, ,
,
因为 ,所以
,所以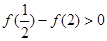 ,即
,即
所以 在区间
在区间 上的最大值是
上的最大值是
综上可知,函数 在区间
在区间 上的最大值是
上的最大值是 ,最小值是0. ……8
,最小值是0. ……8
(3)当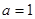 时,
时,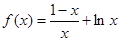 ,
,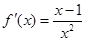 ,故
,故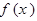 在
在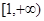 上为增函数.
上为增函数.
当 时,令
时,令 ,则
,则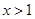 ,故
,故
所以 ,即
,即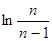 >
>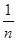
当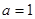 时,对大于1的任意正整数
时,对大于1的任意正整数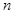 ,有
,有 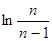 >
>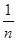
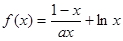 ,所以
,所以
因为函数
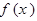 在
在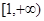 上为增函数,所以
上为增函数,所以 对
对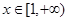 恒成立,
恒成立,所以
 对
对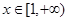 恒成立,即
恒成立,即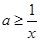 对
对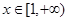 恒成立,所以
恒成立,所以 .……4分
.……4分(2)当
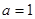 时,
时,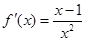 ,所以当
,所以当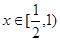 时,
时, ,故
,故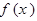 在
在 上单调递减;当
上单调递减;当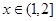 ,
,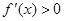 ,故
,故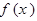 在
在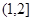 上单调递增,所以
上单调递增,所以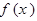 在区间
在区间 上有唯一极小值点,故
上有唯一极小值点,故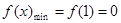 ,又
,又 ,
, ,
, ,
,因为
 ,所以
,所以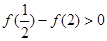 ,即
,即
所以
 在区间
在区间 上的最大值是
上的最大值是
综上可知,函数
 在区间
在区间 上的最大值是
上的最大值是 ,最小值是0. ……8
,最小值是0. ……8(3)当
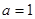 时,
时,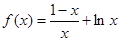 ,
,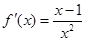 ,故
,故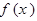 在
在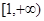 上为增函数.
上为增函数.当
 时,令
时,令 ,则
,则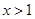 ,故
,故
所以
 ,即
,即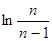 >
>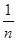
当
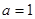 时,对大于1的任意正整数
时,对大于1的任意正整数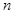 ,有
,有 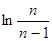 >
>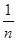
略

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 有一个正根和一个负根,则实数
有一个正根和一个负根,则实数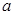 的取值范围是__________________.
的取值范围是__________________.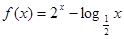 ,且实数
,且实数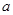 >
>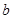 >
>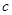 >0满足
>0满足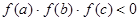 ,若实数
,若实数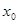 是函数
是函数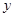 =
=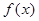 的一个零点,那么下列不等式中不可能成立的是 ( )
的一个零点,那么下列不等式中不可能成立的是 ( )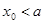
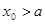

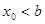
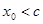
 ,
,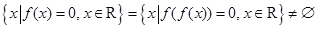 ,则满足条件的所有实数a的取值范围为 ( )
,则满足条件的所有实数a的取值范围为 ( ) <4
<4
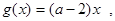 函数
函数 的图像如图所示。
的图像如图所示。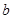 的值;
的值;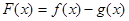 的单调区间。
的单调区间。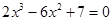 在
在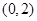 内根的个数有 ( )
内根的个数有 ( ) 天后
天后 的存留量
的存留量 ;若在
;若在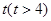 天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量
天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量 随时间变化的曲线恰为直线的一部分,其斜率为
随时间变化的曲线恰为直线的一部分,其斜率为 存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”.
存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”. ,求“二次最佳时机点”;
,求“二次最佳时机点”; 的取值范围.
的取值范围.

 与函数
与函数 的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;  恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围; 〔其中
〔其中 , e为自然对数的底数)
, e为自然对数的底数) 有两个零点、则实数
有两个零点、则实数 的取值范围为__________。
的取值范围为__________。