题目内容
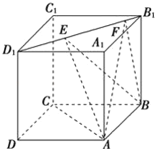
【题目】三棱锥
中，点P是
斜边AB上一点．给出下列四个命题：
①若
平面ABC，则三棱锥的四个面都是直角三角形；
②若S在平面ABC上的射影是斜边AB的中点P，则有
；
③若
，
，
，
平面ABC，则
面积的最小值为3；
④若
，
，，平面ABC，则三棱锥的外接球体积为
．
其中正确命题的序号是__________．(把你认为正确命题的序号都填上)
【答案】①②④.
【解析】
由
平面
，所以
，
，
从而得到四个面都是直角三角形; 连接
,当
平面时，得到
，从而得到
；当
平面时，. 
时，取得最小值，由此求出
的最小值是
;
三棱锥
的外接球可以看作棱长为4的正方体的外接球,
，
，即可求出体积.
对于①，因为平面，所以，，，又
，∴
平面
，所以
，故四个面都是直角三角形，∴①正确；
对于②，由
在平面上的射影是斜边
的中点
，可得平面，连接，有
，
，
，因为P是
斜边AB的中点，所以，故，∴②正确；
对于③，当平面时，
.当时，取得最小值，由等面积可得此时长度为
，所以的最小值是
；∴③不正确；
对于④，若
，平面，∴三棱锥的外接球可以看作棱长为4的正方体的外接球，∴
，，∴体积为
，
④正确，故答案为①②④．
练习册系列答案
全能测控期末小状元系列答案
相关题目
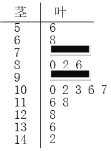
【题目】某校高三期中考试后，数学教师对本次全部学生的数学成绩按1∶20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如下表所示的频率分布表：
分数段（分） |
|
|
|
|
| 总计 |
频数 |
| |||||
频率 |
| 0.25 |
（1）求表中
，
的值及成绩在
范围内的样本数；
（2）从成绩
内的样本中随机抽取4个样本，设其中成绩在
内的样本个数为随机变量
，求的分布列及数学期望
；
（3）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取5个，求其中恰有2个成绩在
内的概率.
