题目内容
(本题满分14分)
已知函数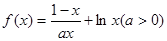
(1)若函数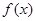 在
在 上为增函数,求实数
上为增函数,求实数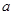 的取值范围
的取值范围
(2)当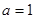 时,求
时,求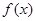 在
在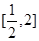 上的最大值和最小值
上的最大值和最小值
(3)求证:对任意大于1的正整数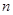 ,
,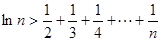 恒成立
恒成立
已知函数
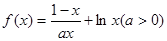
(1)若函数
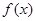 在
在 上为增函数,求实数
上为增函数,求实数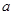 的取值范围
的取值范围(2)当
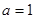 时,求
时,求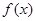 在
在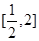 上的最大值和最小值
上的最大值和最小值(3)求证:对任意大于1的正整数
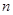 ,
,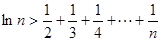 恒成立
恒成立(1)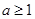 ;(2)
;(2)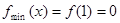 ,
,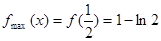 ;(3)见解析。
;(3)见解析。
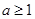 ;(2)
;(2)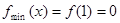 ,
,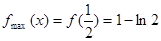 ;(3)见解析。
;(3)见解析。试题分析:(1)先求出函数的导函数,把函数f(x)在[1,+∞)上为增函数转化为导函
数大于等于0恒成立问题,再转化为关于正实数a的不等式问题即可求出正实数a的取值范
围;(2)先求出函数的导函数以及导数为0的根,进而求出其在[
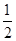 ,2]上的单调性即可
,2]上的单调性即可求f(x)在[
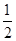 ,2]上的最大值和最小值.(3)运用第一问的结论f(x)>0,放缩法得打对
,2]上的最大值和最小值.(3)运用第一问的结论f(x)>0,放缩法得打对数式的不等式,进而的求和证明。
解:(1)由已知得
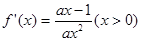 ,依题意得
,依题意得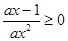 对任意
对任意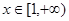 恒成立
恒成立即
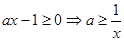 对任意
对任意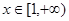 恒成立,而
恒成立,而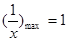
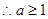
(2)当
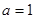 时,
时,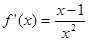 ,令
,令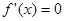 ,得
,得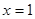 ,若
,若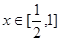 时,
时,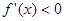 ,若
,若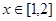 时,
时,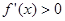 ,故
,故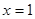 是函数在区间
是函数在区间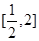 上的唯一的极小值,也是最小值,即
上的唯一的极小值,也是最小值,即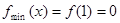 ,而
,而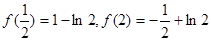 ,
,由于
 ,则
,则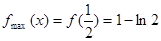
(3)当
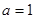 时,由(1)知
时,由(1)知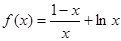 在
在 上为增函数
上为增函数当
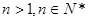 ,令
,令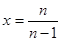 ,则
,则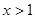 ,所以
,所以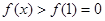
即
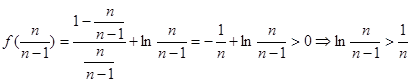
所以
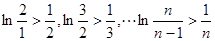
各式相加得
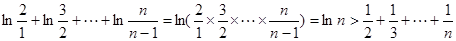
值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到
的,以及利用单调性确定参数范围,不等式的恒成立的证明。
点评:解决该试题的关键是第一问中根据单调递增性,说明了在给定区间的导数恒大于等于
零,得到参数的取值范围。第二问,先求解极值和端点值,比较大小得到结论。

练习册系列答案
相关题目
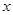 万元,每件产品的成本将降低
万元,每件产品的成本将降低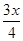 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少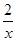 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为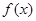 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)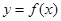 的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则
的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则 的值是
的值是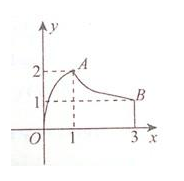
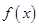 与奇函数
与奇函数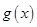 的定义域都是
的定义域都是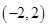 ,它们在
,它们在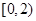 上的图象分别为图(1)、(2)所示,则使关于
上的图象分别为图(1)、(2)所示,则使关于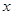 的不等式
的不等式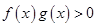 成立的
成立的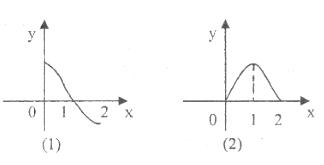
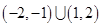
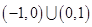
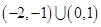
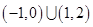
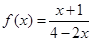 ,则
,则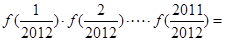 ________
________ 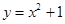 的值域是
的值域是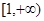
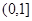
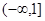
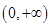
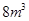 ,深为
,深为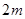 的长方体无盖水池,如果池底和池壁的造价分别为每平方米120元和80元,那么水池的最低总造价是多少元?
的长方体无盖水池,如果池底和池壁的造价分别为每平方米120元和80元,那么水池的最低总造价是多少元?