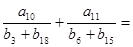题目内容
等差数列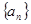 的前
的前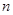 项之和为
项之和为 ,
,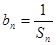 ,且
,且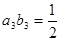 ,
,

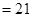 .
.
(1)求数列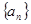 的通项公式;
的通项公式;
(2)求数列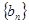 的通项公式;
的通项公式;
(3)求证:
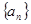 的前
的前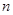 项之和为
项之和为 ,
,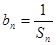 ,且
,且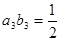 ,
,
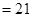 .
.(1)求数列
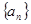 的通项公式;
的通项公式;(2)求数列
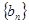 的通项公式;
的通项公式;(3)求证:

(1)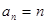 ; (2)
; (2)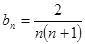 ; (3)证明见解析
; (3)证明见解析
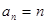 ; (2)
; (2)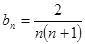 ; (3)证明见解析
; (3)证明见解析(1)将条件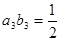 ,
,
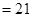 中的多个变量,转化为
中的多个变量,转化为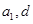 两个变量,从而列方程组求解。(2)等差数列
两个变量,从而列方程组求解。(2)等差数列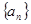 的通项公式解得之后,前
的通项公式解得之后,前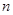 项之和为
项之和为 随之解得,利用
随之解得,利用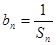 立即可得数列
立即可得数列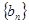 的通项公式.(3)中里利用裂项求和的方式,把
的通项公式.(3)中里利用裂项求和的方式,把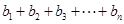 的表达式写出来利用
的表达式写出来利用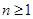 求证。
求证。
解:(1)设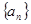 的首项为
的首项为 ,公差为
,公差为 ,有
,有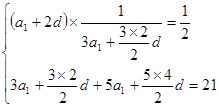 ,解得
,解得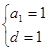
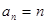 ; ----------4分
; ----------4分
(2)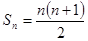 ,
,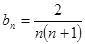 ; -----8分
; -----8分
(3)证明: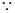
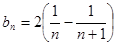 ,
,
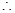

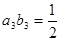 ,
,
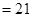 中的多个变量,转化为
中的多个变量,转化为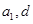 两个变量,从而列方程组求解。(2)等差数列
两个变量,从而列方程组求解。(2)等差数列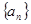 的通项公式解得之后,前
的通项公式解得之后,前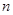 项之和为
项之和为 随之解得,利用
随之解得,利用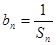 立即可得数列
立即可得数列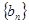 的通项公式.(3)中里利用裂项求和的方式,把
的通项公式.(3)中里利用裂项求和的方式,把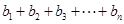 的表达式写出来利用
的表达式写出来利用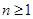 求证。
求证。解:(1)设
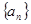 的首项为
的首项为 ,公差为
,公差为 ,有
,有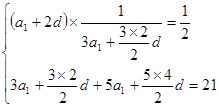 ,解得
,解得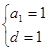
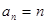 ; ----------4分
; ----------4分(2)
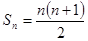 ,
,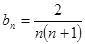 ; -----8分
; -----8分(3)证明:
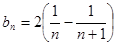 ,
,


练习册系列答案
相关题目
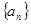 的前
的前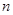 项的和为
项的和为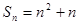 ,
,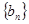 是等比数列,且
是等比数列,且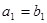 ,
,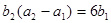 。
。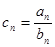 ,求数列
,求数列 的前
的前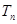 。
。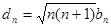 ,数列
,数列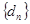 的前
的前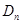 ,求证:
,求证: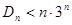 .
.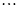 的通项公式
的通项公式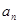 =( )
=( )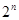
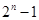
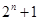

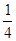
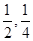
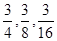
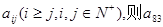 等于 .
等于 . 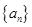 的通项公式
的通项公式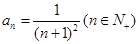 ,
,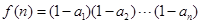 ,试通过计算
,试通过计算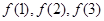 的值,推测出
的值,推测出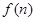 的值。
的值。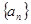 前
前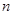 项和为
项和为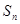 ,且
,且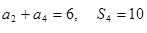
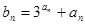 (
(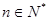 )求数列
)求数列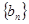 前
前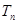
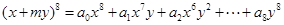 ,若
,若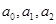 成公差大于0的等差数列,(1)求
成公差大于0的等差数列,(1)求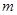 的值;(2)求
的值;(2)求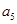 的值;(3)求
的值;(3)求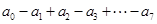 的值.
的值.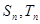 分别是等差数列
分别是等差数列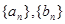 的前
的前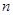 项和,且
项和,且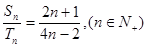 则
则