题目内容
【题目】定义在
上的函数
满足
，
，且当
时，
，则方程
在
上所有根的和为（ ）
A.
B.
C.
D.
【答案】C
【解析】
利用题意可得出函数
的图象关于直线
对称，关于点
对称，并且周期为
，作出图象得知，函数
的图象与函数在
上没有交点，并且函数在
上的图象关于点对称，且函数在区间
上的图象也关于点对称，然后利用对称性得出两个函数交点横坐标之和.
，即
，
，所以，函数是以为周期的周期函数.
又
，则函数的图象关于直线对称.
，
，则函数的图象关于点对称，易知函数的图象也关于点对称，如下图所示：
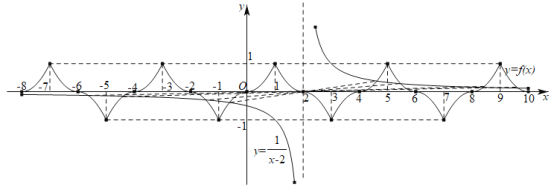
函数的图象与函数在上没有交点，并且函数在上的图象关于点对称，且函数在区间上的图象也关于点对称，两个函数在区间上共有
个公共点，且这些公共点呈现对关于点对称，因此，方程
在
上所有根的和为
.
故选：C.
练习册系列答案
教材全解字词句篇系列答案
相关题目
