题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);以原点
为参数);以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若把曲线![]() 各点的横坐标伸长到原来的
各点的横坐标伸长到原来的![]() 倍,纵坐标变为原来的
倍,纵坐标变为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅲ)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
【答案】(Ⅰ)![]() ,
,![]() .
.
(Ⅱ)![]() .
.
(Ⅲ)![]()
![]() ,此时
,此时![]()
![]()
![]() 的坐标为
的坐标为![]() .
.
【解析】分析:(Ⅰ)直接消参得到直角坐标方程,利用极坐标公式把极坐标化成直角坐标方程.( Ⅱ)利用伸缩变换公式求曲线![]() 的方程.( Ⅲ) 设椭圆上的点
的方程.( Ⅲ) 设椭圆上的点![]() ,再求d的表达式,最后利用三角函数的图像性质求点
,再求d的表达式,最后利用三角函数的图像性质求点![]() 到曲线
到曲线![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
详解:(Ⅰ)由曲线![]() :
:![]() (
(![]() )得
)得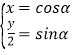 (
(![]() 为参数),
为参数),
∴![]() ,
,
即![]() 为曲线
为曲线![]() 的普通方程.
的普通方程.
由曲线![]()
![]() ,得
,得![]() ,
,
∴![]() 即为
即为![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)依题意,设![]() 是曲线
是曲线![]() 上任意一点,对应曲线
上任意一点,对应曲线![]() 上的点为
上的点为![]() ,
,
则有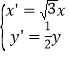 , ∴
, ∴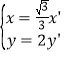 .
.
∵![]() :
: ![]() ,∴
,∴![]() .
.
即所求曲线![]() 的方程为
的方程为![]() .
.
(Ⅲ)易知,椭圆![]() 与直线
与直线![]() 无公共点,设椭圆上的点
无公共点,设椭圆上的点![]() ,
,
从而点![]() 到直线
到直线![]() 的距离为
的距离为
![]()
![]()
![]()
∴当![]() 时,
时,![]() ,
,
此时![]() ,
,![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗
