题目内容
已知椭圆
+
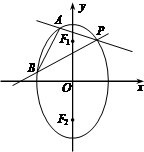
=1两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足
•
=1,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
(1)求P点坐标;
(2)求证:直线AB的斜率为定值;
(3)求△PAB面积的最大值.

| x2 |
| 2 |
| y2 |
| 4 |
| PF1 |
| PF2 |
(1)求P点坐标;
(2)求证:直线AB的斜率为定值;
(3)求△PAB面积的最大值.

(1)由题可得F1(0,
),F2(0-
),
设P0(x0,y0)(x0>0,y0>0)
则
=(-x0,
-y0),
=(-x0,-
-y0)(2分)
∴
•
=
-(2-
)=1,
∵点P(x0,y0)在曲线上,则
+
=1,
∴
=
,从而
-(2-
)=1,得y0=
.
则点P的坐标为(1,
).(5分)
(2)证明:由题意知,两直线PA、PB的斜率必存在,设PB的斜率为k(k>0),(6分)
则BP的直线方程为:y-
=k(x-1).
由
得(2+k2)x2+2k(
-k)x+(
-k)2-4=0,
设B(xB,yB),则1+xB=
,xB=
-1=
,
同理可得xA=
,则xA-xB=
,yA-yB=-k(xA-1)-k(xB-1)=
.(9分)
所以AB的斜率kAB=
=
为定值.(10分)
(3)设AB的直线方程:y=
x+m.
由
,得4x2+2
mx+m2-4=0,
由△=(2
m)2-16(m2-4)>0,得-2
<m<2
P到AB的距离为d=
,(12分)
则S△PAB=
|AB|•d=
•
=
≤
=
.
当且仅当m=±2∈(-2
,2
)取等号
∴△PAB面积的最大值为
.(14分)
| 2 |
| 2 |
设P0(x0,y0)(x0>0,y0>0)
则
| PF1 |
| 2 |
| PF2 |
| 2 |
∴
| PF1 |
| PF2 |
| x | 20 |
| y | 20 |
∵点P(x0,y0)在曲线上,则
| ||
| 2 |
| ||
| 4 |
∴
| x | 20 |
4-
| ||
| 2 |
4-
| ||
| 2 |
| y | 20 |
| 2 |
则点P的坐标为(1,
| 2 |
(2)证明:由题意知,两直线PA、PB的斜率必存在,设PB的斜率为k(k>0),(6分)
则BP的直线方程为:y-
| 2 |
由
|
| 2 |
| 2 |
设B(xB,yB),则1+xB=
2k(k-
| ||
| 2+k2 |
2k(k-
| ||
| 2+k2 |
k2-2
| ||
| 2+k2 |
同理可得xA=
k2+2
| ||
| 2+k2 |
4
| ||
| 2+k2 |
| 8k |
| 2+k2 |
所以AB的斜率kAB=
| yA-yB |
| xA-xB |
| 2 |
(3)设AB的直线方程:y=
| 2 |
由
|
| 2 |
由△=(2
| 2 |
| 2 |
| 2 |
P到AB的距离为d=
| |m| | ||
|
则S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
(4-
|
| |m| | ||
|
|
|
| 2 |
当且仅当m=±2∈(-2
| 2 |
| 2 |
∴△PAB面积的最大值为
| 2 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

