题目内容
直平行六面体ABCD-A1B1C1D1的棱长均为2，∠BAD=60°，则对角线A1C与侧面DCC1D1所成角的正弦值为( )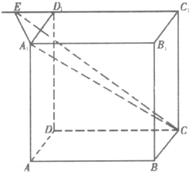
A．
B. 
C．
D．
D
解析：本题考查线面角的求法．作A1E⊥C1D1交C1D延长线于点E，连结CE，∵DD1⊥面A1B1C1D1
∴A1E⊥DD1 ∴A1E⊥面CC1D1D，
∴∠A1CE即为A1C与面CC1D1D所成的角，且AC2=AB2+BC2-2ABBCcosl20°=12 A1C2=+A1C2=4+12=16
A1C=4 A1E=A1D1sin60°=2×=
∴sin∠A1CE=.
练习册系列答案
阅读快车系列答案
相关题目
如图：直平行六面体ABCD-A1B1C1D1，底面ABCD是边长为2a的菱形，∠BAD=60°，E为AB中点，二面角A1-ED-A为60°．
如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中，∠BAD=60°，长为2的线段MN的一个端点M在DD1上运动，另一个端点N在底面ABCD上运动，则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为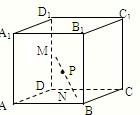
已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中，∠BAD=60°，长为2的线段MN的一个端点M在DD1上运动，另一个端点N在底面ABCD上运动．则MN中点P的轨迹与该直平行六面体表面所围成的几何体中较小体积值为（ ）
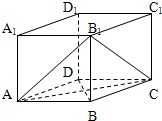如图，在直平行六面体ABCD-A1B1C1D1中，底面对角线BD与各条棱长都相等，则二面角B1-AC-B的大小为