题目内容
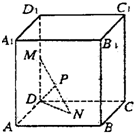
 如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为
如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为| 2π |
| 9 |
| 2π |
| 9 |
分析:先推导点P的轨迹,从而确定点P与平行六面体所围成的几何体的形状,然后求几何体的体积
解答: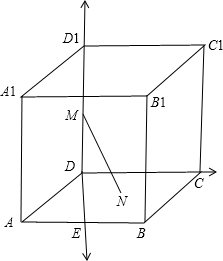 解:取AB的中点E连接DE,由题意知DE⊥AB,DE⊥CD
解:取AB的中点E连接DE,由题意知DE⊥AB,DE⊥CD
以DE所在直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立如图空间直角坐标系
设M(0,0,z),N(x,y,0),则P(
,
,
)
MN=
=2
∴x2+y2+z2=4
∴
+
+
=(
)2+(
)2+(
)2=1
∴OP2=1
即OP=1
∴点P的轨迹是以原点D为球心,以1为半径的球的一部分
又∵∠BAD=60°
∴∠ADC=120°
∴点P的轨迹是球的
∴几何体的体积为V=
×
π×13=
故答案为:
 解:取AB的中点E连接DE,由题意知DE⊥AB,DE⊥CD
解:取AB的中点E连接DE,由题意知DE⊥AB,DE⊥CD以DE所在直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立如图空间直角坐标系
设M(0,0,z),N(x,y,0),则P(
| x |
| 2 |
| y |
| 2 |
| z |
| 2 |
MN=
| x2+y2+z2 |
∴x2+y2+z2=4
∴
| x2 |
| 4 |
| y2 |
| 4 |
| z2 |
| 4 |
| x |
| 2 |
| y |
| 2 |
| z |
| 2 |
∴OP2=1
即OP=1
∴点P的轨迹是以原点D为球心,以1为半径的球的一部分
又∵∠BAD=60°
∴∠ADC=120°
∴点P的轨迹是球的
| 1 |
| 6 |
∴几何体的体积为V=
| 1 |
| 6 |
| 4 |
| 3 |
| 2π |
| 9 |
故答案为:
| 2π |
| 9 |
点评:本题考查几何体的体积,须先用代数法确定点的轨迹,然后熟练应用体积公式即可.属中档题

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为________.
如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为________.