题目内容
棱长都为2的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,则对角线A1C与侧面DCC1D1所成角的余弦值为
.
| ||
| 4 |
| ||
| 4 |
分析:作A1E⊥C1D1,垂足为E,则可得对角线A1C与侧面DCC1D1所成角,从而可求对角线A1C与侧面DCC1D1所成角的余弦值.
解答: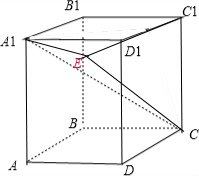 解:作A1E⊥C1D1,垂足为E,连CE,A1E,A1C.
解:作A1E⊥C1D1,垂足为E,连CE,A1E,A1C.
∵ABCD-A1B1C1D1是直平行六面体
∴A1E⊥平面DCC1D1,
∴∠A1CE就是对角线A1C与侧面DCC1D1所成角
∵CE?平面A1B1C1D1,
∴A1E⊥CE
∵棱长都为2的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,
∴A1E=2sin60°=
,D1E=1
∴A1C1=2
∴A1C=4
∴CE=
在Rt△A1EC中,cos∠A1CE=
=
故答案为:
 解:作A1E⊥C1D1,垂足为E,连CE,A1E,A1C.
解:作A1E⊥C1D1,垂足为E,连CE,A1E,A1C.∵ABCD-A1B1C1D1是直平行六面体
∴A1E⊥平面DCC1D1,
∴∠A1CE就是对角线A1C与侧面DCC1D1所成角
∵CE?平面A1B1C1D1,
∴A1E⊥CE
∵棱长都为2的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,
∴A1E=2sin60°=
| 3 |
∴A1C1=2
| 3 |
∴A1C=4
∴CE=
| 13 |
在Rt△A1EC中,cos∠A1CE=
| CE |
| A1C |
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题重点考查线面角,解题的关键是利用线面垂直,作出线面角,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目