题目内容
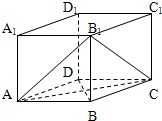 如图,在直平行六面体ABCD-A1B1C1D1中,底面对角线BD与各条棱长都相等,则二面角B1-AC-B的大小为
如图,在直平行六面体ABCD-A1B1C1D1中,底面对角线BD与各条棱长都相等,则二面角B1-AC-B的大小为arctan2
arctan2
.分析:由已知中,直平行六面体ABCD-A1B1C1D1中,底面对角线BD与各条棱长都相等,根据二面角的定义,我们可得∠B1OB即为二面角B1-AC-B的平面角,解Rt△B1OB,即可求出二面角B1-AC-B的大小.
解答:解:连接AC交BD于O,连接B1O
由直平行六面体ABCD-A1B1C1D1中,底面对角线BD与各条棱长都相等
可得AC⊥B1O,且AC⊥BO
故∠B1OB即为二面角B1-AC-B的平面角,
设对角线BD与各条棱长都为1
则在Rt△B1OB中,B1B=1,OB=
则tan∠B1OB=2
故∠B1OB=arctan2
故答案为:arctan2
由直平行六面体ABCD-A1B1C1D1中,底面对角线BD与各条棱长都相等
可得AC⊥B1O,且AC⊥BO
故∠B1OB即为二面角B1-AC-B的平面角,
设对角线BD与各条棱长都为1
则在Rt△B1OB中,B1B=1,OB=
| 1 |
| 2 |
则tan∠B1OB=2
故∠B1OB=arctan2
故答案为:arctan2
点评:本题考查的知识点是与二面角有关的立体几何综合问题,其中根据已知条件及二面角的定义,确定∠B1OB即为二面角B1-AC-B的平面角,是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
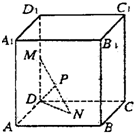
 如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为
如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为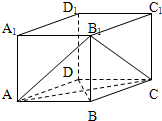 如图,在直平行六面体ABCD-A1B1C1D1中,底面对角线BD与各条棱长都相等,则二面角B1-AC-B的大小为________.
如图,在直平行六面体ABCD-A1B1C1D1中,底面对角线BD与各条棱长都相等,则二面角B1-AC-B的大小为________.