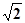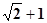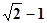题目内容
已知直线
 与抛物线
与抛物线 相交于
相交于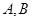 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若 ,则k的值为( )。
,则k的值为( )。
A. | B. | C. | D. |
D
解析试题分析:抛物线 的准线方程为
的准线方程为 ,设
,设 ,因为
,因为 ,根据抛物线上的点到焦点的距离等于到准线的距离,可得:
,根据抛物线上的点到焦点的距离等于到准线的距离,可得: ,
,
联立直线方程和抛物线方程可得: ,根据韦达定理可得:
,根据韦达定理可得: ,与
,与 联立可得
联立可得
考点:本小题主要考查直线与抛物线的位置关系.
点评:解决与抛物线有关的问题时,要注意抛物线上的点的最重要的性质是到焦点的距离等于到准线的距离,要灵活应用.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
过M(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有( )条
| A.0 | B.1 | C.2 | D.4 |
若抛物线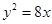 上一点
上一点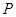 到其焦点的距离为
到其焦点的距离为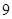 ,则点
,则点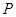 的坐标为( )
的坐标为( )
A.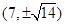 | B.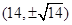 | C.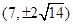 | D.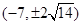 |
抛物线 的焦点坐标是
的焦点坐标是
A. | B. | C. | D. |
如果 表示焦点在
表示焦点在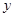 轴上的椭圆,那么实数
轴上的椭圆,那么实数 的取值范围是( )
的取值范围是( )
A.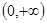 | B.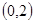 | C.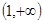 | D.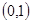 |
已知F1,F2为双曲线C: 的左右焦点,点P在C上,
的左右焦点,点P在C上, ,则
,则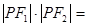 ( )
( )
| A. 2 | B. 4 | C. 6 | D. 8 |
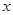 的不等式
的不等式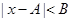 的解集叫
的解集叫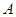 的
的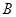 邻域.已知
邻域.已知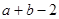 的
的 邻域为区间
邻域为区间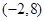 ,其中
,其中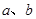 分别为椭圆
分别为椭圆 的长半轴和短半轴.若此椭圆的一焦点与抛物线
的长半轴和短半轴.若此椭圆的一焦点与抛物线 的焦点重合,则椭圆的方程为( . )
的焦点重合,则椭圆的方程为( . ) 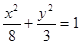
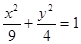
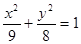
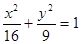
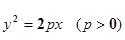 的焦点F恰好是双曲线
的焦点F恰好是双曲线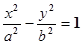 的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )