题目内容
【题目】在数列![]() 中,
中,![]() ,且对任意
,且对任意![]() ,
,![]() 成等差数列,其公差为
成等差数列,其公差为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,证明
,证明![]() 成等比数列(
成等比数列(![]() );
);
(3)若对任意![]() ,
,![]() 成等比数列,其公比为
成等比数列,其公比为![]() ,设
,设![]() ,证明数列
,证明数列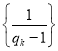 是等差数列.
是等差数列.
【答案】(1)![]() ,
,![]() .(2)见证明;(3)见证明;
.(2)见证明;(3)见证明;
【解析】
(1)由![]() 成等差数列且公差为2可计算
成等差数列且公差为2可计算![]() 的值.
的值.
(2)由![]() 可得
可得![]() ,再根据
,再根据![]() 得到
得到![]() ,从而可证
,从而可证![]() 成等比数列.
成等比数列.
(3)利用![]() 成等比数列且公比为
成等比数列且公比为![]() 可得
可得![]() ,对该递推关系变形后可得
,对该递推关系变形后可得 为等差数列.
为等差数列.
(1)因为对任意![]() ,
,![]() 成等差数列,
成等差数列,
所以当![]() 时,
时,![]() 成等差数列且公差为2,
成等差数列且公差为2,
故![]() ,故
,故![]() .
.
(2)证明:由题设,可得![]() ,
,![]() .所以
.所以![]()
![]() ,
,
由![]() 得,
得,![]() ,
,
从而![]() ,所以
,所以![]() .
.
于是![]() ,
,
所以当![]() 时,对任意的
时,对任意的![]() ,
,![]() 成等比数列.
成等比数列.
(3)由![]() 成等差数列,及
成等差数列,及![]() 成等比数列,
成等比数列,
可得![]() ,所以
,所以![]() ,
,
当![]() 时,可知
时,可知![]() ,
,![]() ,
,
从而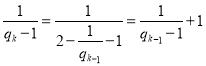 ,即
,即![]() ,
,
所以数列 是公差为1的等差数列.
是公差为1的等差数列.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目