题目内容
5.已知平面直角坐标系中,点O为原点,A(-3,-4),B(5,-12).(1)求$\overrightarrow{AB}$的坐标及|$\overrightarrow{AB}$|;
(2)若$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,$\overrightarrow{OD}$=$\overrightarrow{OA}-\overrightarrow{OB}$,求$\overrightarrow{OC}$,$\overrightarrow{OD}$的坐标;
(3)求cos<$\overrightarrow{OA}$,$\overrightarrow{OC}$>
分析 (1)利用向量坐标运算、模的计算公式即可得出;
(2)利用向量的坐标运算即可得出;
(3)利用向量夹角公式夹角即可得出.
解答 解:(1)$\overrightarrow{AB}$=$\overrightarrow{OB}-\overrightarrow{OA}$=(5,-12)-(-3,-4)=(8,-8),
∴$|\overrightarrow{AB}|$=$\sqrt{{8}^{2}+(-8)^{2}}$=8$\sqrt{2}$.
(2)$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$=(-3,-4)+(5,-12)=(2,-16),
$\overrightarrow{OD}$=$\overrightarrow{OA}-\overrightarrow{OB}$=(-3,-4)-(5,-12)=(-8,8).
(3)cos<$\overrightarrow{OA}$,$\overrightarrow{OC}$>=$\frac{\overrightarrow{OA}•\overrightarrow{OC}}{|\overrightarrow{OA}||\overrightarrow{OC}|}$=$\frac{-6+64}{\sqrt{{3}^{2}+{4}^{2}}\sqrt{{2}^{2}+1{6}^{2}}}$=$\frac{29\sqrt{65}}{325}$.
点评 本题考查了向量坐标运算、模的计算公式、向量夹角公式夹角,属于基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
20.已知向量$\overrightarrow{a}$=(-2,2),$\overrightarrow{b}$=(-8,6),平面向量$\overrightarrow{c}$满足$\overrightarrow{a}$•$\overrightarrow{c}$=0,$\overrightarrow{b}$•$\overrightarrow{c}$=2,则$\overrightarrow{c}$等于( )
| A. | (1,2) | B. | (-1,-2) | C. | (1,1) | D. | (-1,-1) |
14.在区间[-1,5]上任取一个数x,则log2(x+3)≥log2(3x+4)-1的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
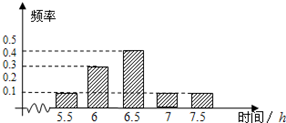 某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.
某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示. 如图,△ABC内接于圆O,直线L平行AC交线段BC于D,交线段AB于E,交圆O于G、F,交圆O在点A的切线于P.若D是BC的中点,PE=6,ED=4,EF=6,则PA的长为2$\sqrt{6}$.
如图,△ABC内接于圆O,直线L平行AC交线段BC于D,交线段AB于E,交圆O于G、F,交圆O在点A的切线于P.若D是BC的中点,PE=6,ED=4,EF=6,则PA的长为2$\sqrt{6}$.