题目内容
15.已知椭圆中心在原点,焦点在x轴上,F1,F2分别是它的左、右焦点,A是椭圆上一点,且$\overrightarrow{{F}_{1}{F}_{2}}$$•\overrightarrow{A{F}_{1}}$=0,|$\overrightarrow{{F}_{1}{F}_{2}}$|=$\frac{4}{3}$|$\overrightarrow{A{F}_{1}}$|,则椭圆的离心率为$\frac{1}{2}$.分析 由题意,$\overrightarrow{{F}_{1}{F}_{2}}$$•\overrightarrow{A{F}_{1}}$=0,可得$\overrightarrow{{F}_{1}{F}_{2}}$⊥$\overrightarrow{A{F}_{1}}$,|$\overrightarrow{A{F}_{1}}$|=$\frac{{b}^{2}}{a}$,利用|$\overrightarrow{{F}_{1}{F}_{2}}$|=$\frac{4}{3}$|$\overrightarrow{A{F}_{1}}$|,可得2c=$\frac{4}{3}$×$\frac{{b}^{2}}{a}$,即可求出椭圆的离心率.
解答 解:由题意,$\overrightarrow{{F}_{1}{F}_{2}}$$•\overrightarrow{A{F}_{1}}$=0,可得$\overrightarrow{{F}_{1}{F}_{2}}$⊥$\overrightarrow{A{F}_{1}}$,∴|$\overrightarrow{A{F}_{1}}$|=$\frac{{b}^{2}}{a}$,
∵|$\overrightarrow{{F}_{1}{F}_{2}}$|=$\frac{4}{3}$|$\overrightarrow{A{F}_{1}}$|,
∴2c=$\frac{4}{3}$×$\frac{{b}^{2}}{a}$,
∴3ac=2(a2-c2),
∴2e2+3e-2=0,
∴e=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$
点评 本题考查椭圆的离心率,考查向量知识的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
10.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1,作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
7.双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的左、右顶点分别为A1,A2,点P在C上且直线PA2的斜率的取值范围是($\frac{1}{2}$,1),那么直线PA1斜率的取值范围是( )
| A. | ($\frac{1}{3}$,$\frac{3}{4}$) | B. | ($\frac{3}{4}$,$\frac{5}{2}$) | C. | ($\frac{1}{3}$,$\frac{5}{2}$) | D. | ($\frac{5}{4}$,$\frac{5}{2}$) |
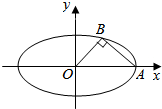 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,O为坐标原点,点B在C上,△OBA为等腰直角三角形.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,O为坐标原点,点B在C上,△OBA为等腰直角三角形.